the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Free-flow wind speed from a blade-mounted flow sensor
Torben Juul Larsen
Helge Aagaard Madsen
Søren Juhl Andersen
This paper presents a method for obtaining the free-inflow velocities from a 3-D flow sensor mounted on the blade of a wind turbine.
From its position on the rotating blade, e.g. one-third from the tip, a blade-mounted flow sensor (BMFS) is able to provide valuable information about the turbulent sheared inflow in different regions of the rotor. At the rotor, however, the inflow is affected by the wind turbine, and in most cases the wind of interest is the inflow that the wind turbine is exposed to, i.e. the free-inflow velocities.
The current method applies a combination of aerodynamic models and procedures to estimate the induced velocities, i.e. the disturbance of the flow field caused by the wind turbine. These velocities are subtracted from the flow velocities measured by the BMFS to obtain the free-inflow velocities. Aeroelastic codes, like HAWC2, typically use a similar approach to calculate the induction, but they use it for the reversed process, i.e. they add the induction to the free inflow to get the flow velocities at the blades, which are required to calculate the resulting aerodynamic forces.
The aerodynamic models included in the current method comprise models based on blade element momentum (BEM) for axial and tangential induction, a radial induction model and tip loss correction, and models for skew and dynamic inflow.
It is shown that the method is able to calculate the free-inflow velocities with high accuracy when applied to aeroelastic HAWC2 simulations with a stiff structural model while some deviations are seen in simulations with a flexible structure.
Furthermore, the method is tested on simulations performed by a flexible structural model coupled with a large-eddy simulation (LES) flow solver. The results of this higher-fidelity verification confirm the HAWC2-based conclusion.
- Article
(8553 KB) - Full-text XML
- BibTeX
- EndNote
Detailed knowledge about the atmospheric turbulent wind and its variation is essential for understanding and analysing many aspects regarding wind turbines, e.g. load conditions, power generation, noise aspects, and fatigue and extreme loads (Barlas et al., 2012; Elliott and Cadogan, 1990; Larsen et al., 2005; Madsen, 2014; St. Martin et al., 2016)
The wind of interest is the free undisturbed turbulent inflow, but at the location of the wind turbine rotor. The problem is that this free wind is immeasurable, as the inflow is influenced by the presence of the rotor itself: near the turbine, the flow is disturbed by the turbine, and further away, the wind is different. The ideal measure, therefore, is the free-flow wind speed at the position of the turbine, i.e. the wind speed as it would have been at the same location and time without the turbine.
A cup or sonic anemometer at a nearby met mast, e.g. 2–3 diameters away, measures the free-flow wind when not in the wake of the turbine or the mast, but smaller turbulence structures will be different due to the distance. As these structures have only limited influence on 10 min statistics, the wind speeds measured by met masts are still valuable and extensively used.
The wind speed measured by a nacelle- or spinner-mounted anemometer is influenced by the turbine. This influence is measurable more than one diameter upstream (Meyer Forsting et al., 2017) and continues until the wake is recovered far downstream. This means that a model or calibration function is required to estimate the free-flow wind speed from a nacelle- or spinner-mounted anemometer.
The turbine is, however, not only exposed to the wind at the hub centre, and with the long blades of modern wind turbines, the wind-speed variations within the rotor may be considerable. This variation can be measured using lidars, which are typically ground or nacelle based. From the nacelle, a lidar is able to measure the inflow field some distance upstream while the inflow field at the rotor plane can be measured using a set of ground-based scanning lidars (Mikkelsen et al., 2008, 2010; Scholbrock et al., 2015; Wagner et al., 2015). Nevertheless, the problem is the same; the lidars must either measure outside the induction zone to measure the free inflow or use a model to compensate for the presence of the turbine. Troldborg and Meyer Forsting (2017) describe a simple analytical model that is able to estimate the free wind speed, appropriate for power curves, from lidar measurements. The model is applicable for any rotor down to one rotor radius upstream.
Another option is to mount a flow sensor directly on the blade, e.g. one-third from the tip. From this location, the sensor sweeps the rotor area and is thereby able to measure a lot of the variation that takes place within the rotor area. The sensor may be mounted closer to the root or the tip, but closer to the root it will only sweep a smaller part of the rotor, and near the tip it will suffer from severe blade deflection and tip-loss effects. Furthermore, the load distribution along the blade should be taken into account, such that the sensor measures the inflow where the largest loads occur. In Pedersen et al. (2017), different radial positions are investigated and 50–67 was found to be optimal.
Blade-mounted five-hole pitot tubes have been used in several research projects (Brand et al., 1996; Hand et al., 2001; Madsen, 1991; Madsen et al., 2003, 2010b; Medina et al., 2011; Petersen and Madsen, 1997; Schepers et al., 2002; Simms et al., 1999), but other types of sensors could be used as well. In the current context, a blade-mounted flow sensor (BMFS) is assumed to measure the 3-D inflow velocity at its position, i.e. the temporal resolution of a point fixed in space is limited to once per revolution, and multiple sensors are required for measuring in both the inner and outer parts of the rotor. From the 3-D inflow velocities measured by a BMFS, information about the angle of attack, relative velocity and the instant wind speed at the rotor plane can be extracted. This information can be used as input for the control of individual pitch or active trailing edge flaps to optimize power and reduce loads and noise (Barlas et al., 2012; Kragh and Hansen, 2012; Kragh et al., 2012; Larsen et al., 2005; Madsen, 2014). Another application is the generation of relative power or load curves that can be compared between similar periods or turbines. These relative curves can be used to investigate aerodynamic modifications or detect performance issues, for example (Pedersen et al., 2017).
As a BMFS is inside the induction zone, a model is required to estimate the free-flow wind speed. In this case, however, well-defined models already exist as they are used in aeroelastic codes, e.g. HAWC2, to simulate the flow that generates the aerodynamic forces at the blades (Larsen and Hansen, 2007; Madsen et al., 2018). These models calculate the disturbance of the flow caused by the turbine in terms of the induced velocities, which are then added to the free-flow velocity to get the disturbed wind speed at the blades. Reversing this process, the free-flow wind speed can be obtained by subtracting the induced velocities from the measured velocities.
This paper describes the necessary aerodynamic models as well as a procedure to obtain an estimate of the free-flow velocity from a BMFS. This estimate provides information about the mean wind speed variations within the rotor, the turbulence and the instant wind speed history. This information can be used to characterize the inflow conditions that result in low power or high loads, for example, and as input for aeroelastic simulations to improve the correlation between the measured and simulated loads. A preliminary implementation of the method has previously been applied to measurements of a full-scale wind turbine with a blade-mounted five-hole pitot tube to estimate the free inflow and shear profiles in different wake conditions (Pedersen et al., 2015).
To test the method, both the disturbed and the immeasurable free-flow wind speeds are required. A real validation against measurements is therefore infeasible. Instead, the method is tested in two different simulated environments.
The first environment is simulated by HAWC2, a nonlinear aeroelastic code intended for computing wind turbine response in the time domain (Larsen and Hansen, 2007). HAWC2 uses Taylor's well-known frozen turbulence hypothesis (Taylor, 1938) and a combination of aerodynamic models, which are similar to the models of the current method, to calculate the disturbed flow velocity at the rotor plane. Both the free inflow and the disturbed flow at the rotor plane are therefore directly available for verification of the method.
In the second environment, the simulations are performed by the structural model of FLEX5 (Øye, 1996) coupled with the large-eddy simulation (LES) flow solver, EllipSys3D (Michelsen, 1992; Sørensen, 1995). This environment is completely independent of the aerodynamic models of the current method as well as Taylor's frozen turbulence hypothesis and is therefore valuable as a high-fidelity verification. In this case, the free undisturbed inflow is obtained from a separate equivalent simulation in which the effects of the aerodynamic forces on the flow are disabled.
This section presents the aerodynamic models and the procedure used to obtain the free-inflow velocities from a BMFS.
2.1 Coordinate systems
The coordinate systems used in this paper are listed in Table 1.
Transformation matrices are used to map velocities between the coordinate systems. As an example, the transformation matrix, TRG, describes the rotating-rotor coordinate-system axes in ground coordinates. TRG can be used to map velocities in rotor coordinates, VR, to velocities in ground coordinates, VG:
2.2 Wind speed from a BMFS
The method described in this paper takes as input the effective 3-D inflow velocities measured relative to the blade, locally at the rotor plane, i.e. including the effects caused by the presence of the turbine.
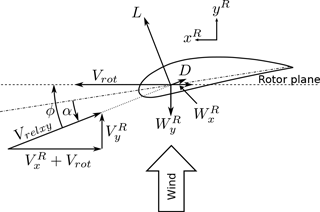
Near the airfoil, the local flow field is deflected and the speed is also influenced by the bound circulation on the surface of the airfoil; see the example in Fig. 1. As seen, this effect has a huge impact on the flow velocity measured near the airfoil and must therefore be compensated for before applying the current method. In the current study, however, it is neglected as the two verification environments, HAWC2 and EllipSys3D–Flex5, do not model the surface of the airfoils.
Shen et al. (2006, 2009), Guntur and Sørensen (2014), and Rahimi et al. (2018) present several methods to calculate the flow near the airfoil that also take 3-D effects into account, but the methods require information that cannot be obtained directly from a BMFS. Pedersen et al. (2017) describes how to obtain the effective 3-D inflow from the relative wind speed and two perpendicular angles measured by a blade-mounted five-hole pitot, including compensation for bound circulation. The compensation method uses a look-up table generated by 2-D computational fluid dynamic (CFD) simulations, thus neglecting 3-D effects and tip and root vortices.

Figure 1Near the airfoil, the flow is disturbed by upwash and stagnation. This effect is not included in the current method.
From the relative velocity, Vrel, the wind speed at the rotor plane, Vr, is found by adding the velocity of the sensor, Vs:
In this study, the sensor velocity, Vs, includes movement due to rotor rotation and pitch motion. Structural dynamics, e.g. blade deflection, will therefore result in a mismatch between the assumed and the actual sensor velocity.
2.3 Aerodynamic models
The wind speed measured in the rotor plane of an operating wind turbine is different from the free-flow wind speed that would have been present at the same time and location if the wind turbine was absent. The difference is induced by the wind turbine and is rather complex. In this section, a set of simplified engineering aerodynamic models that each explain elements of the induction are presented. One can argue that the models are too simple compared to the physical processes. In general, however, the loads simulated by aeroelastic codes that use these models are found to agree well with measured loads; see e.g. Larsen et al. (2013). The models are therefore expected to be appropriate for the reverse process too.
The aerodynamic models in aeroelastic codes like FAST, Flex5, Bladed and HAWC2 are based on the blade element momentum (BEM) model first presented by Glauert (1935). The original formulation, however, was derived for axis-symmetric, steady and uniform inflow, which is far from the conditions that a real turbine operates in. The BEM model is therefore typically modified and combined with additional sub-models, e.g. for tip loss and for skew and dynamic inflow. In this study, the aerodynamic model is based on the HAWC2 implementation (Madsen et al., 2018).
2.3.1 Axial induction
When operating, a wind turbine extracts kinetic energy from the wind by reducing the axial wind speed. This reduction is called the axial induction, ; see Fig. 2.
The axial-induced wind speed is defined in terms of the axial induction factor, a:
where V0 is the free-inflow velocity.
For laminated flow through the rotor, the axial induction factor is related to the thrust coefficient, CT, by
while empirical results show higher values of CT for induction factors above 0.3–0.5 (Eggleston and Stoddard, 1987). The current method uses a third-order polynomial, as described by Madsen et al. (2018),
with coefficients and k1=0.2460 that fit to Eq. (4) for lower values of a and to empirical results and actuator disc simulations for higher loading (Madsen et al., 2010a).
For an annular ring element at radius r, the thrust coefficient is calculated using the formula presented by Madsen et al. (2018):
where Vrelxy is the relative wind speed in the (xR,yR) plane (see Fig. 3), c is the chord length, α is the angle of attack, NB is the number of blades and Cy is the projection of the lift and drag coefficient into yR:
where is the angle between Vrelxy and the rotor plane.
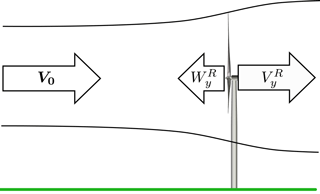
Figure 2At the rotor plane, the free-inflow wind velocity, V0, is reduced by the axial induction, . A sensor at the rotor plan will therefore measure the reduced velocity, , in the axial direction.
From the measurements of a BMFS, Vrelxy and α can be obtained directly, and the number of blades, the pitch angle, the radius, the chord length and the blade twist angle are assumed to be known. Hence, if the angle-of-attack-dependent lift and drag coefficients are accessible from a look-up table, then the only unknown term on the right-hand side of Eq. (6) is V0.
In aeroelastic simulations, V0 is obtained from the wind input model, but in this case, V0 is the wind speed that we want to find. It can, however, be found using the iterative approach described in Sect. 2.4, such that the induced axial velocity can be calculated via Eqs. (6), (5) and (3).
2.3.2 Tip correction
The relationship between the thrust coefficient and the axial induction factor stated in Eq. (4) is based on the assumption that the induced velocities are constant within an annular element. This is not the case for turbines with a finite number of blades and therefore Prandtl's tip loss factor, presented by Glauert (1935),
where R is the blade tip radius, is applied in the current method by replacing CT with in Eq. (5) as described by Madsen et al. (2018). Calculating and applying the tip loss factor is straightforward as the only variable on the right-hand side, ϕ, can be calculated from the BMFS output.
2.3.3 Tangential induction
The tangential induction is a reaction to the torque force and results in a rotation of the wake downstream. The tangential velocity of the wake is defined in terms of the tangential induction factor, a′:
where ω is the angular velocity of the rotor.
Variations in the tangential flow due to blade passing can be observed more than one rotor radius upstream. This effect is, however, assumed to be handled by the compensation for deflection and change of flow speed near the airfoil, which is required before the current method is applied (see Sect. 2.2). The current tangential induction model only describes the reaction to the wake rotation that starts near the blades and increases downstream. This effect is assumed to be insignificant upstream. The amount of wake rotation at the position of a BMFS is therefore dependent on the sensor position relative to the blade, the pitch angle and the blade-deflection state. The current implementation of the method assumes full tangential induction, but for some applications, it may be more appropriate to switch it off.
The tangential induction factor is obtained by the formula presented by Madsen et al. (2018):
where is the projection of the lift and drag coefficient into xR; see Fig. 3.
In Eq. (10), the only unknown term on the right-hand side is also V0, which can be found via the iterative approach described in Sect. 2.4. To help this iterative procedure in finding the right solution, the value of a used in Eq. (10) is limited to the range [0;0.5].
2.3.4 Radial induction
The radial induction results in an expansion of the flow, as illustrated in Fig. 2. Introducing the radial induction factor, ar, the radially induced velocity is
The standard one-dimensional BEM theory does not handle radial induction and therefore the analytical equation derived by Madsen et al. (2010a) is used in the current method:
where CT,avg is the average thrust coefficient of the whole rotor. In the current model, the revolution-averaged local thrust coefficient of the BMFS is used. This is obviously not the same, and the approximation is therefore only appropriate if the thrust coefficient of the radial position corresponds to the average thrust coefficient of the whole rotor. This is typically not the case near the root and the tip, and even for a sensor that is one-third from the tip, some discrepancies must be expected.
2.3.5 Dynamic inflow
The induced velocities are part of an equilibrium which is gradually established between the load on the blades, the rotor wake and the induced velocity at the rotor plane (Sørensen and Madsen, 2006).
Small- and high-frequency turbulence is assumed to pass unaffected though the rotor and can therefore be measured directly, while the effect of large stationary turbulence eddies can be described by the BEM models in Sect. 2.3.1 and 2.3.3. In between, the modification of the wind flow depends on the wake recovery velocity. Snel and Schepers (1995) present different engineering approaches to model the wind turbine response in dynamic inflow.
In the current method, the model used in HAWC2 (Madsen et al., 2018) has been implemented with two modifications. This implementation applies two first-order low-pass filters to the induced velocities to model the slow and gradually changing induction,
where LP(τ,X) is a first-order low-pass filter. The two filters model the near- and far-wake effects respectively, and their filter characteristics are given by the following.
where
Equations (16) and (17) can be calculated straight away, while V0 and are required for Eqs. (14) and (15). V0 can be estimated as described in Sect. 2.4, while the instant average axial induction of the whole rotor, , requires information from the whole rotor, which cannot be obtained from a BMFS.
In the current implementation, the revolution-averaged local induction is used as an approximation. This means that the filter characteristics may be inaccurate if the induction at the radial position of the BMFS is not representative for the whole blade. The sensitivity to is, however, limited and even extreme values have only a minor impact on the final estimated free wind speed.
The other modification is more severe. In HAWC2, the rotor is discretized in grid points and the dynamic inflow model is applied to the local induced velocities of each of these grid points. This is possible because the local induction is calculated for each grid point in every time step, and this means that the induction of a certain grid point reflects the current circumstances as well as the history of that particular grid point.
In the current method, only the local induction at the position of the BMFS is obtainable as no information is available from other parts of the rotor. Applying the dynamic inflow model to the induced velocities at the position of the BMFS means that the estimated induction reflects the history of the moving BMFS instead of a fixed position. In a situation with wind shear, the estimated induction will therefore be too high in the lower part of the rotor and too low in the upper part, resulting in too much variation in the estimated free wind speed.
Instead, the low-pass filters are applied to the induced wind speeds of fixed azimuthal positions. As the BMFS only passes a certain azimuthal position once per revolution, the sample frequencies of these signals are very low and some discrepancies must be expected.
Figure 4 shows the induced velocities in a simulation with turbulent inflow and shear. The quasi-steady induced velocities estimated without the dynamic inflow model, , are seen to vary much more than the HAWC2 reference, while applying the low-pass filters to the rotating measurements, , smoothens the induction too much. Applying the low-pass filters to the low-frequency signals of fixed azimuthal positions, , results in an estimate closer to the HAWC2 reference even though there is still some mismatch.
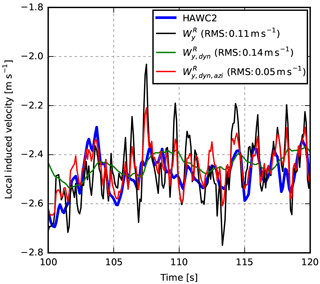
Figure 4Local induced axial velocity calculated using HAWC2 and the current method in three configurations: W without the dynamic inflow model (), with the dynamic inflow model applied to the rotating measurements (), and with the dynamic inflow model applied to the low-frequency signals of fixed azimuthal positions ().
2.3.6 Skew inflow
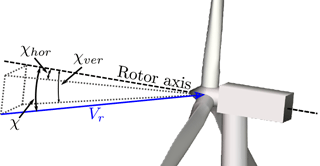
In skewed inflow, where the mean wind is not perpendicular to the rotor plane due to yaw misalignment, rotor tilt and flow inclination, for example, the axial induction is not directed exactly towards the wind. Hence the speed of the inflow is reduced less, and the thrust is increased. Furthermore, variation in the wake vorticity concentration results in an azimuthal-dependent variation in the axial induction; see Fig. 5.
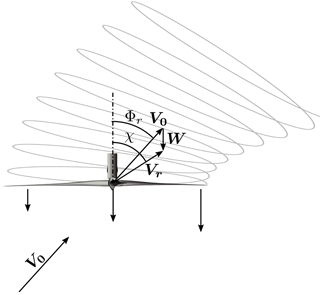
Figure 5Wind turbine in skew inflow. The axial induction varies due to different wake vorticity concentration, and it is not directed exactly towards the wind.
The first effect is modelled by the method described in Madsen et al. (2018) where the axial induction factor is multiplied by a reduction factor, Fa, that is calculated from the average thrust coefficient, CT,avg, and the skew inflow angle, Φr.
where
The average thrust coefficient is estimated using the revolution-averaged local thrust coefficient as described in Sect. 2.3.4, and in this case the approximation is also expected to introduce discrepancies. The inflow angle, Φr, which is the angle between the inflow and the rotor axis, i.e. it includes effects of both horizontal and vertical skew inflow, is calculated by
Note that the CT,avg used in Eq. (18) must be limited to the range [0;1] as the model is invalid outside this range.
The azimuthal variation is calculated with a model presented by Madsen et al. (2018). In this model, the axial induction factor is multiplied with a rotor-position-dependent factor, Fazi:
where θrotor is the rotor-azimuth position. The factors kx and ky depend on the inflow angle in the horizontal and vertical plane, χhor and χver, respectively; see Fig. 6:
2.3.7 Combining models
The presented aerodynamic models are now combined into a function, fW, that comprises the following steps.
-
Calculate CT using Eq. (6).
-
Calculate the tip loss factor with Eq. (8).
-
Calculate a with Eq. (5) replacing CT with .
-
Apply the skew inflow model by
-
Calculate the tangential induction factor using Eq. (10).
-
Calculate the radial induction factor using Eq. (12).
-
Calculate the quasi-steady induced velocities .
-
Apply the dynamic inflow model by
Using this function, the estimated induced velocities can be calculated for a given V0,
2.4 Estimating V0
The flow velocity measured by the BMFS is the sum of the free-flow and the induced velocities, hence
Using fW, defined in Sect. 2.3.7, an estimate of the free-flow velocity can be obtained.
Figure 7 shows the estimated free wind speed, , as a function of in an example in which the measured wind speed, is around 9.6 m s−1.
We now want to find the correct free wind speed, i.e. the V0, that, when inserted into Eq. (29), results in V0,est being equal to V0 (12 m s−1 in Fig. 7). In other words, we iteratively solve
with respect to V0 using the Newton–Raphson method and Vr as the initial guess for V0.
2.5 Verification
2.5.1 HAWC2
The method is verified using HAWC2 simulations of a Siemens 3.6 MW turbine with a 107 m rotor. The turbine has a 6∘ tilt and 3.5∘ coning angle and is controlled by the basic DTU Wind Energy controller (Hansen and Henriksen, 2013). The inflow turbulence for the turbulence cases is generated using the Mann model (Mann, 1994).
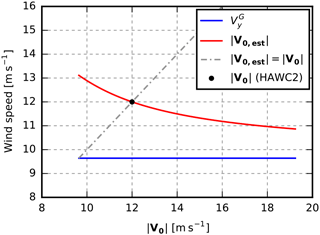
Figure 7Example of free wind speed estimation. For , the estimated free wind speed, , calculated with Eq. (29) equals .
From the simulations, the relative wind speed is extracted at a point on the blade at radius 36 m, i.e. around one-third from the tip. From this wind speed the estimated free wind speed is calculated and compared to the free wind speed used as the input to HAWC2. Note that the current version of HAWC2 (version 12.5) does not include radial induction, and therefore this model is disabled when testing against HAWC2.
As the current method is based on the same aerodynamic models as HAWC2, one may argue that this verification just adds and subtracts the same value, which obviously results in the original velocity. There are, however, differences that are important to investigate, e.g. the effect of the differences and approximation in the aerodynamic models of the current method, the effect of a flexible structure and the V0-estimation procedure.
2.5.2 EllipSys3D–Flex5
The method is furthermore verified using EllipSys3D–Flex5 simulations of a 2.3 MW Siemens turbine with a 93 m rotor. In these simulations, the flow field is obtained from LES performed by the finite-volume and incompressible Navier–Stokes solver, EllipSys3D (Michelsen, 1992; Sørensen, 1995). The turbine is modelled using the actuator line method as developed by Sørensen and Shen (2002), in which the individual blades are modelled by imposing body forces into the flow solver. The actuator lines are fully coupled to the aeroelastic tool, Flex5 (Øye, 1996), which models the structural dynamics according to the incoming flow; see Sørensen et al. (2015) for details on the coupling. The inflow turbulence, which is similar to the turbulence of the HAWC2 simulations, is imposed 8.25 radius upstream from the rotor.
From these simulations, the flow speed is extracted at radius 32 m, i.e. also around one-third from the tip. All EllipSys3D–Flex5 simulations use a flexible structural model. Flex5 is based on modal shape functions as opposed to the multibody formulation of HAWC2 and hence does not include torsional rotation of the blades.
To obtain the free-inflow velocities, a separate identical flow simulation is performed, in which the effect of the aerodynamic forces on the flow is disabled such that the flow is not affected by the turbine. From this simulation the flow field in the vertical plane through the rotor centre is obtained for each time step.
In the aeroelastic HAWC2 simulations, the 3-D correction method by Snel et al. (1993) is applied to the tabulated lift-coefficient polars, while the actuator line simulations have been run without 3-D corrections. The current method relies on the same tabulated polars, and additional uncertainty must therefore be expected if the method is applied to fully resolved CFD simulations or real measurements due to discrepancies of the tabulated lift and drag coefficients and due to the 3-D effects not taken into account. Furthermore, it should be noted that the two verification environments are not totally independent as both rely on tabulated lift and drag coefficient polars.
2.5.3 Free-flow reference
The estimated free-flow velocities are based on the velocities measured at the sensor position (red dot in Fig. 8). In the current verification, however, the reference free-flow velocity is extracted at the assumed (un-deflected) sensor position (green dot in Fig. 8). This mismatch is expected to introduce some deviation as the turbulence is different at the two positions.
In the HAWC2 simulations, which are based on Taylor's frozen turbulence hypothesis, the turbulence is transported unaffected by the mean wind, i.e. with constant (free flow) speed along the yG axis. This means that time can be mapped into space and the free-flow velocities can be extracted from the 3-D turbulence field that is generated prior to the simulation.
The EllipSys flow, however, includes properties of real flow, e.g. turbulence structures change and break up over time. The 3-D turbulence field will therefore change in every time step and only the velocities at the rotor-centre flow plane are available for this study. The assumed sensor position, however, does not exactly intersect this plane due to the rotor tilt angle. We are therefore compelled to rely on Taylor's frozen turbulence hypothesis to obtain the free-flow reference velocity at the assumed sensor position, but only from the rotor-centre plane to the sensor position (blue arrow in Fig. 8), i.e. at most 3.3 m.
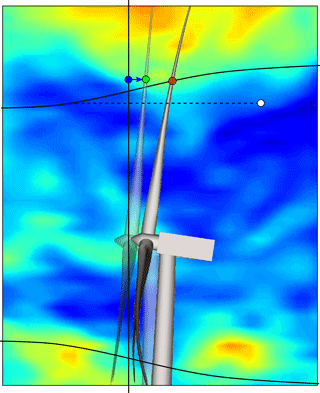
Figure 8The estimated free flow at the sensor position (red dot) is compared to the free flow at the assumed position (green dot). In the EllipSys3D–Flex5 simulations, the nearest available free-flow velocity is at the rotor-centre plane (blue dot). The sensor is, however, exposed to “delayed” turbulence structures that originate from a smaller radial position (white dot).
Furthermore, the EllipSys flow is affected by the turbine. Near the rotor, the axial induction reduces the turbulence transport speed, while the radial induction results in an expansion of the flow that moves the turbulence structure outwards.
This means that the BMFS is exposed to “delayed” turbulence structures that originate from a smaller radial position (white dot in Fig. 8), and even more deviation is therefore expected.
3.1 HAWC2 verification
The root-mean-squared error, RMS, of the estimated instantaneous free wind speed, V0,est, is shown for 7 m s−1 in Fig. 9 for HAWC2 simulations of increasing complexity and the EllipSys3D–Flex5 simulations.
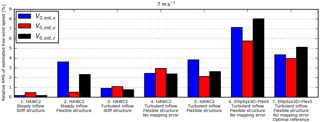
Figure 9Relative RMS of the estimated free wind speed at 7 m s−1. For Cases 4, 6 and 7, “no mapping error” means that deviations introduced in the transformation from the deflected blade-section coordinates to the fixed ground coordinates are not included.
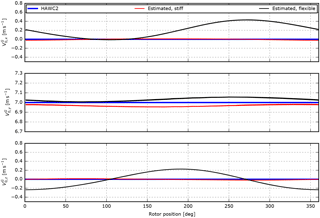
Figure 10HAWC2 results including the free wind speed estimated in 13 m s−1 steady uniform inflow for stiff (Case 1) and flexible (Case 2) structural models.
Starting with steady, uniform inflow and a stiff structural model, Case 1, the RMS error is very small and the minor deviations between the estimated free velocities and the HAWC2 references in Fig. 10 are caused by the effects of rotor tilt that are not exactly compensated for by the skew inflow model.
In Case 2, the structural model is flexible. The rotation of the sensor due to the deflection and torsion of the tower and blade results in increased error levels that are clearly seen in the x and z velocity components in Fig. 10.
The most significant error is the 90∘ phase-shifted sinusoidal oscillation of the estimated velocities. This error is caused by thrust-dependent flap-wise deflection of the blade that results in a part of being inaccurately projected onto the zR direction; see Fig. 11. This constant error leads to oscillations of the x and z components in the non-rotating ground coordinate system.
This error is reduced by a counteracting effect, namely the torque pushing the blade forward in the edge-wise direction. At this forward-pushed position, the direction of the actual velocity due to rotor rotation, , is slightly changed, but the blade-section coordinate system is rotated even more as seen in the right-hand side of Fig. 12. A small part of is thereby measured in the radial −zR direction, while the current model assumes the rotational velocity, Vrot, to be tangential. This mismatch leads to a torque-dependent error in the −zR direction that reduces the thrust-dependent contribution from flap-wise deflection.
A closer look at Fig. 10 reveals a positive offset in the estimated x component. The reason for this offset, which corresponds to a spurious side wind, is a combination of two effects, both caused by gravity-induced edge-wise deflections of the blade. When the blades are horizontal, the gravity pulls the blades down towards the earth; see the left- and right-hand sides of Fig. 12. This asymmetric edge-wise deflection leads to a small part of being measured in the radial −zR direction on the right-hand side of the rotor and in the +zR direction on the left-hand side, i.e. in the +xG direction on both sides. Furthermore, the transition from backward to forward deflection results in the blade moving faster in the upper part of the rotor and vice versa in the lower part. In the current method, however, the assumed rotational speed, Vrot, is uniform. The mismatch results in deviations that also map to +xG in both vertical positions; see Fig. 12.
In combination, these two effects result in the almost constant positive offset of the velocity seen in Fig. 10.
For higher wind speeds, the estimated free wind speed in the yG direction is overestimated due to the rotation of the elastic blade section. As the rotation angles are unknown in the current method, an error is introduced in the transformation from blade-section to ground coordinates; see Fig. 13. Blade torsion is an obvious source of the rotation, but for the current turbine model flap-wise bending also contributes considerably. This effect is highly dependent on the wind speed and blade design, and for the DTU 10 MW reference wind turbine (Bak et al., 2013), an underestimation was seen instead.
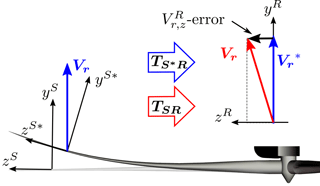
Figure 11The rotation angle of the deflected blade section is unknown in the current method. An error is thereby introduced when mapping the measured wind speed, Vr, from the blade-section to the rotating-rotor coordinates using the transformation matrix, TSR. The result is a constant error in the zR direction that leads to sinusoidal oscillations of the x and z components of the estimated free wind speed seen in Fig. 10.
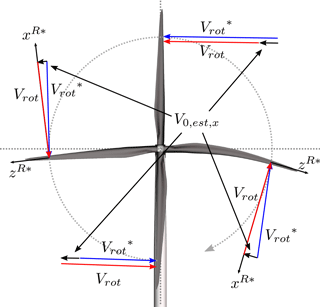
Figure 12When the blades are horizontal, a small part of is measured in the direction on the right-hand side of the rotor and in the direction on the left-hand side due to the gravity-induced deflection of the blade section. Furthermore, the blade moves faster in the upper part of the rotor due to the transition from backward to forward deflection and slower in the lower part. In the current method, however, the rotational speed, Vrot, is assumed to be tangential and uniform. The mismatch results in a spurious side wind, seen as a mean offset in the x component of Fig. 10.
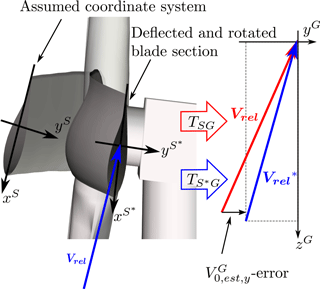
Figure 13The torsion angle of the deflected blade section is unknown in the current method. An error is thereby introduced when mapping the relative velocity, Vrel, from the blade-section to the ground coordinates using the transformation matrix, TSG. The result is the overestimation of the y component of the estimated free wind speed, .
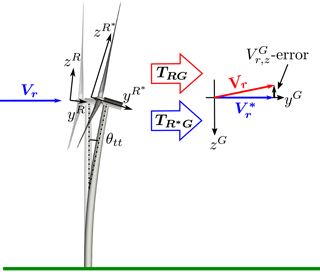
Figure 14The tower-top deflection angle, θtt, is unknown in the current method, and therefore the applied transformation matrix, TRG, inaccurately projects a small part of Vr onto . The result is the small negative offset in the z component in Fig. 10.
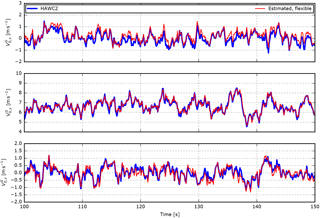
Figure 15HAWC2 results include the free wind speed estimated in turbulent inflow for a flexible structural model (Case 5).
Another effect that is seen in higher wind speeds is a negative mean offset in the z component due to tower deflection. In the transformation from rotating-rotor to ground coordinates, the angle between yR and yG is assumed to equal the tilt angle, but due to tower deflection the real angle is slightly larger, as it also includes the tower-top deflection angle, θtt; see Fig. 14. A small part of Vr is therefore inaccurately projected onto zG, resulting in a small error in .
This error can easily be compensated for by including the tower-top deflection angle, measured by an inclinometer, in the transformation from rotating-rotor to ground coordinates. Similarly, the blade deflection and torsion angles can be included in the transformation from blade-section to rotor coordinates. These angles are, however, more challenging to measure due to the large centrifugal force.
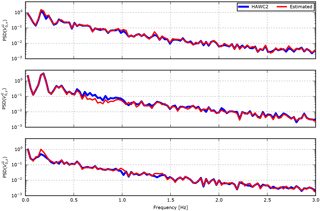
Figure 16HAWC2 results including the power spectrum density of the free wind speed estimated in turbulent inflow for a flexible structural model.
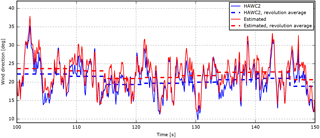
Figure 17HAWC2 results including the wind direction derived from estimated free wind speed and HAWC2 reference in a simulation with 20∘ yaw misalignment.
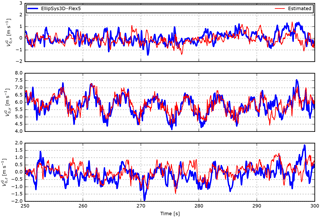
Figure 18EllipSys3D–Flex5 results including the free wind speed estimated in velocity based on turbulent inflow (7 m s−1) in blade-section coordinates (Case 6).
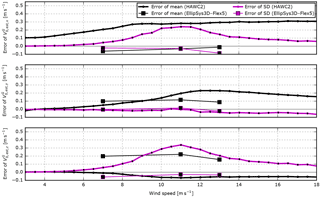
Figure 19The difference between the mean/SD of the free wind speed at the position of the sensor and the mean/SD of the estimated free wind speed. The HAWC2 results are based on 10 min of simulations of the Siemens 3.6 MW turbine. The deviations are mainly introduced in the mapping of velocities from the deflected blade-section coordinate system to the ground coordinate system. The EllipSys3D–Flex5 results are based on 200 s of simulations of the Siemens 2.3 MW turbine. In this case, the deviations are mainly introduced by differences in the induction modelling approach. Both results are obtained from simulations of a flexible structure in turbulent inflow without shear.
In Case 3, a stiff structural model is simulated in turbulent inflow. In this case, the estimated free-inflow velocities fall almost on top of the HAWC2 reference despite the differences in the dynamic inflow model.
Case 4 combines the flexible structure with turbulent inflow, but the BMFS-measured flow velocities are extracted in the ground coordinates such that errors introduced in the transformation from deflected blade-section coordinates are avoided. The errors are significantly increased in all components; see Fig. 9. The reason is the mismatch between the assumed sensor velocity, i.e. the velocity due to rotor rotation and pitch motion, and the real velocity, which also includes velocity due to dynamic deflections of the structure. Furthermore, deviations are introduced because the free-flow reference velocity is extracted at the assumed (un-deflected) sensor position, while the model estimates the velocity at the deflected sensor position; see Fig. 8. This mismatch can be reduced, assuming that the real sensor position can be measured, e.g. using a GPS, or estimated with a method that includes tower and blade deflection.
In Case 5, the BMFS-measured flow velocities are extracted in deflected blade-section coordinates and error is introduced due to the unknown orientation of this coordinate system; see Figs. 9 and 15. Higher RMS errors are therefore expected, but in this case, the error of the y component is reduced because the error due to coordinate transformation counteracts the error introduced by dynamic deflections. Note that this reduction is highly dependent on the turbine design as it depends on the actual flap and twist properties of the blade, and for other designs the error may be increased instead.
Figure 16 shows the power spectrum density of Case 5. The 1P (once per revolution) oscillating errors seen in the x and z components in Fig. 10 are seen around 0.2 Hz, while the deviations caused by dynamic deflections are seen in the y component above 0.4 Hz. At first it seems strange that the energy of the y component of the estimated free wind speed is lower than the HAWC2 reference, as the additional velocity due to the movement of the BMFS is expected to increase the energy. In reality, however, the deflection of the structure is correlated with the turbulence, as a blade exposed to a gust will deflect. This means that a BMFS that measures the gust relative to the deflecting blade will measure a less-severe gust with less energy.
Figure 17 shows the instant and revolution-averaged wind direction in a simulation with 20∘ yaw misalignment. The estimated wind direction is seen to follow the HAWC2 reference with a few degrees offset due to the spurious side wind caused by gravity-induced edge-wise blade deflections.
Case 6 is based on the EllipSys3D–Flex5 simulations. The RMS errors are higher than in Case 4, which is the most equivalent HAWC2 case. Note, however, that the numbers are not directly comparable due to the different turbine sizes. The time series are compared in Fig. 18.
For the last case, Case 7, an optimization routine was used to find the optimal reference position with respect to axial and radial offset. For the 7 m s−1 the lowest RMS error was found when the estimated free velocities were compared to the free flow that hits the rotor-centre plane 2.2 s before and 4.2 m closer to the rotor centre. As seen in Fig. 9, the error is significantly reduced in all components. It is therefore concluded that the relatively high error of Case 6 is more related to the difference between the turbulence at the sensor and the reference position than to deviations introduced in the aerodynamic models and free-flow estimation procedure.
Finally, Fig. 19 shows the difference between the free mean wind speed and estimated free mean wind speed at the position of the sensor, and similarly for the standard deviation. The HAWC2 results are based on 10 min of simulations of the Siemens 3.6 MW turbine. The deviations are mainly introduced in the mapping of velocities from the deflected blade-section coordinate system to the ground coordinate system. The EllipSys3D–Flex5 results are based on 200 s of simulations of the Siemens 2.3 MW turbine. These velocities are extracted in ground coordinates; i.e. deviations due to mapping are not included. In Fig. 18, instantaneous deviations are seen, mainly because the turbulence at the sensor position is different from the free-flow turbulence at the reference position due to expansion, delay and evolvement of the flow. In this case, however, most of these deviations are averaged out, and the error in Fig. 19 is mainly introduced by differences in the induction modelling approach.
The error introduced in the transformation from deflected blade-section coordinates to ground coordinates is clearly seen in all components of the HAWC2 results. In the x component, the rotor speed and torque-dependent spurious side wind increases the error of the mean wind speed up to rated rotor speed (around 9 m s−1). In the y component, the overestimation due to blade torsion is seen. The error in the mean wind speed in the z direction, due to tower deflection, increases with the thrust up to rated wind speed (around 11 m s−1). Above rated wind speed, the error is rather constant as increased drag on the tower counterbalances the decrease in thrust. Finally, the error, due to flap-wise deflection of the blades, that results in the 1P oscillating deviations of the x and z components is clearly seen in the error of the standard deviation, which peaks with the thrust around rated wind speed.
In this paper, a method to estimate the undisturbed free-inflow velocities from the flow velocities measured by a blade-mounted flow sensor, BMFS, has been presented and verified. The method includes a combination of aerodynamic models and procedures to estimate the free-flow velocities from the measurements of a BMFS. The aerodynamic models comprise BEM-based models for axial and tangential induction, a radial induction model and tip loss correction, and models for skew and dynamic inflow. Some of these models require information, e.g. the average thrust coefficient of the whole rotor, that cannot be obtained from a BMFS. In these cases, approximations are used even though they are expected to introduce errors. Most of the models also take as input the free wind speed, which is the final output of the current method. An iterative procedure is therefore used to find the estimated free wind speed.
The method has been verified on HAWC2 simulations. This verification reveals that the method works well and provides accurate results when using a stiff structural model. Using a flexible structural model, larger deviations are seen. These deviations are caused by the rotation of the sensor due to the deflection and torsion of the tower and blade, movement of the sensor due to turbulence-induced dynamic deflections of the structure, and the mismatch between the turbulence at the real deflected sensor position and the reference position, i.e. the assumed (un-deflected) sensor position. These effects are highly dependent on the wind speed and the structural design.
Furthermore, the method has been verified by simulations performed using EllipSys3D–Flex5: a flexible structural model coupled with a large-eddy simulation (LES) flow solver. In these results, the free velocities estimated using the current method deviate more from the simulated free velocities, but it is concluded that the error is more related to the difference between the turbulence at the sensor and the reference position than to errors introduced in the aerodynamic models and free-flow estimation procedure.
Applied to real measurements, additional uncertainty must be expected due to mounting, calibration and sensor uncertainty, discrepancy of the tabulated lift and drag coefficients, and 3-D effects not taken into account.
Simulation results are not available due to confidentiality.
| a | Axial induction factor |
|---|---|
| a′ | Tangential induction factor |
| ar | Radial induction factor |
| c | Chord length |
| CT | Trust coefficient |
| CT,avg | Average trust coefficient |
| Cx | Lift and drag coefficient projected into xR |
| Cy | Lift and drag coefficient projected into yR |
| D | Aerodynamic drag force |
| Fa | Thrust reduction factor in skew inflow model |
| Fazi | Azimuthal-dependent reduction factor in skew inflow model |
| Ftip | Prandtl's tip loss factor |
| fW | Function calculating induced velocities |
| ki, i=0…3 | Constants |
| kx, ky | Factors in skew inflow model |
| L | Aerodynamic lift force |
| LP(τ,X) | Low-pass filter with filter characteristics, τ |
| NB | Number of blades |
| r | Sensor radius |
| R | Blade tip radius |
| Tab | Transformation matrix from coordinate system a to coordinate system b |
| Vr | Measured flow velocity at rotor plane |
| Vrel | Measured velocity relative to the sensor |
| Vrelxy | Relative wind speed in the (xR,yR) plane |
| Vrot | Velocity of sensor due to rotor rotation |
| Vs | Velocity of the sensor |
| V0 | Free-flow wind speed |
| V0,est | Estimated free-flow wind speed |
| W | Induced velocity |
| West | Estimated induced velocity |
| Wavg | Average induced velocity |
| Wdyn | Induced velocity, estimated using dynamic inflow model |
| Wdyn,azi | Induced velocity, estimated using dynamic inflow model applied to fixed azimuthal positions |
| α | Angle of attack |
| χ | Angle between Vr and rotor axis |
| χhor | Horizontal angle between Vr and rotor axis |
| χver | Vertical angle between Vr and rotor axis |
| ω | Angular rotor velocity |
| ϕ | Angle between rotor plane and Vrelxy |
| Φr | Angle between rotor plane and V0 |
| θpitch | Pitch angle |
| θrotor | Rotor azimuthal position |
| θtt | Tower-top deflection angle |
| θtwist | Twist angle |
| Coordinate systems; see Sect. 2.1 | |
| G | Ground coordinate system |
| R | Rotating-rotor coordinate system |
| S | Blade-section coordinate system |
| Modifiers | |
| * | Actual velocity or deflected direction (opposed to the assumed velocity or un-deflected direction) |
The authors declare that they have no conflict of interest.
The authors would like to acknowledge Siemens Wind Power for providing data
for the simulation model.
Edited by: Luciano
Castillo
Reviewed by: Vasilis A. Riziotis and Walter Gutierrez
Bak, C., Zahle, F., Bitsche, R., Kim, T., Yde, A., Henriksen, L. C., Hansen, M. H., Blasques, J. P. A. A., Gaunaa, M., and Natarajan, A.: The DTU 10-MW Reference Wind Turbine, Tech. rep., presented at Danish Wind Power Research 2013, Fredericia, Denmark, 27 May 2013, available at: http://www.orbit.dtu.dk (last access: 20 March 2018), 2013. a
Barlas, T., van der Veen, G., and van Kuik, G.: Model predictive control for wind turbines with distributed active flaps: incorporating inflow signals and actuator constraints, Wind Energy, 15, 757–771, https://doi.org/10.1002/we.503, 2012. a, b
Brand, A., Dekker, J., de Groot, C., and Späth, M.: Overview of aerodynamic measurements on an Aerpac 25 WPX wind turbine blade at the HAT 25 experimental wind turbie, ECN-DE-Memo-96-014, Energy research Centre of the Netherlands (ECN), Petten, the Netherlands, 1996. a
Eggleston, D. M. and Stoddard, F. S.: Wind turbine engineering design, Van Nostrand Reinhold, New York, USA, 1987. a
Elliott, D. L. and Cadogan, J. B.: Effects of wind shear and turbulence on wind turbine power curves, in: Wind Energy, 10–14, Pacific Northwest Lab., Richland, WA (USA), Presented at the European Community Wind Energy Conference and Exhibition, Madrid, Spain, 10–14 September 1990, available at: http://www.osti.gov/scitech/servlets/purl/6348447 (last access: 20 March 2018), 1990. a
Glauert, H.: Airplane Propellers, 169–360, Springer Berlin Heidelberg, Berlin, Heidelberg, https://doi.org/10.1007/978-3-642-91487-4_3, 1935. a, b
Guntur, S., and Sørensen, N. N.: An evaluation of several methods of determining the local angle of attack on wind turbine blades, J. Phys. Conf. Ser., 555, 12045, https://doi.org/10.1088/1742-6596/555/1/012045, 2014. a
Hand, M. M., Simms, D. A., Fingersh, L. J., Jager, D. W., and Cotrell, J. R.: Unsteady aerodynamics experiment phase V: test configuration and available data campaigns, Tech. rep., National Renewable Energy Lab, available at: https://www.nrel.gov/docs/fy01osti/29491.pdf (last access: 20 March 2018), 2001. a
Hansen, M. H. and Henriksen, L. C.: Basic DTU Wind Energy controller, Tech. rep., DTU Wind Energy, available at: http://www.orbit.dtu.dk (last access: 20 March 2018), 2013. a
Kragh, K. and Hansen, M.: Individual Pitch Control Based on Local and Upstream Inflow Measurements, in: 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Reston, Virigina, Aerospace Sciences Meetings, 9–12 January 2012, American Institute of Aeronautics and Astronautics, https://doi.org/10.2514/6.2012-1021, 2012. a
Kragh, K. A., Henriksen, L. C., and Hansen, M. H.: On the Potential of Pitch Control for Increased Power Capture and Load Alleviation, in: Torque, the science of making torque from wind, Presented at The Science of Making Torque from Wind 2012, 9–11 October 2012, Oldenburg, Germany, available at: http://www.orbit.dtu.dk (last access: 20 March 2018), 2012. a
Larsen, T. J. and Hansen, A. M.: How 2 HAWC2, the user's manual, no. December in Denmark. Forskningscenter Risoe. Risoe-R, Technical Report, Risø National Laboratory, Roskilde, Denmark, available at: http://www.orbit.dtu.dk (last access: 20 March 2018), 2007. a, b
Larsen, T. J., Madsen, H. A., and Thomsen, K.: Active load reduction using individual pitch, based on local blade flow measurements, Wind Energy, 8, 67–80, https://doi.org/10.1002/we.141, 2005. a, b
Larsen, T. J., Madsen, H. A., Larsen, G. C., and Hansen, K. S.: Validation of the dynamic wake meander model for loads and power production in the Egmond aan Zee wind farm, Wind Energy, 16, 605–624, https://doi.org/10.1002/we.1563, 2013. a
Madsen, H. A.: Risø-M-2902: Aerodynamics and Structural Dynamics of a Horizontal Axis WindTurbine – Raw Data Overview, Technical Report Risø-M-2902, Risø National Laboratory, Roskilde, Denmark, 1991. a
Madsen, H. A.: Correlation of amplitude modulation to inflow characteristics, Proceedings of 43rd International Congress on Noise Control Engineering, Inter-noise 2014, Melbournen Australia, 16–19 November 2014, available at: http://www.acoustics.asn.au/conference_proceedings/INTERNOISE2014/papers/p171.pdf (last access: 20 March 2018), 2014. a, b
Madsen, H. A., Thomsen, K., and Petersen, S. M.: Risø-I-210: Wind Turbine Wake Data from Inflow Measurements using a Five hole Pitot Tube on a NM80 Wind Turbine Rotor in the Tjæreborg Wind Farm, Technical Report Risø-I-2108, Risø National Laboratory, Roskilde, Denmark, 2003. a
Madsen, H. A., Bak, C., Døssing, M., Mikkelsen, R. F., and Øye, S.: Validation and modification of the Blade Element Momentum theory based on comparisons with actuator disc simulations, Wind Energy, 13, 373–389, https://doi.org/10.1002/we.359, 2010a. a, b
Madsen, H. A., Bak, C., Schmidt Paulsen, U., Gaunaa, M., Fuglsang, P., Romblad, J., Olesen, N. A., Enevoldsen, P., Laursen, J., and Jensen, L.: The DAN-AERO MW Experiments: Final report, Denmark. Forskningscenter Risoe. Risoe-R, Danmarks Tekniske Universitet, Risø Nationallaboratoriet for Bæredygtig Energi, available at: http://www.orbit.dtu.dk (last access: 20 March 2018), 2010b. a
Madsen, H. A., Larsen, T. J., Pirrung, G., Verelst, D., and Zahle, F.: An implementation of the BEM model for simulation of non-uniform loading and inflow, in press, 2018. a, b, c, d, e, f, g, h, i
Mann, J.: The spatial structure of neutral atmospheric surface-layer turbulence, J. Fluid Mech., 273, 141, https://doi.org/10.1017/S0022112094001886, 1994. a
Medina, P., Singh, M., Johansen, J., Jove, A. R., Machefaux, E., Fingersh, L. J., and Schreck, S.: Aerodynamic and performance measurements on a SWT-2.3-101 wind turbine, Tech. rep., National Renewable Energy Laboratory (NREL), Golden, CO., 2011. a
Meyer Forsting, A. R., Troldborg, N., Murcia Leon, J. P., Sathe, A., Angelou, N., and Vignaroli, A.: Validation of a CFD model with a synchronized triple-lidar system in the wind turbine induction zone, Wind Energy, 20, 1481–1498, https://doi.org/10.1002/we.2103, 2017. a
Michelsen, J. A.: Basis3D – a Platform for Development of Multiblock PDE Solvers, Tech. rep., Danmarks Tekniske Universitet, Kongens Lyngby, Denmark, 1992. a, b
Mikkelsen, T., Mann, J., Courtney, M., and Sjöholm, M.: Windscanner: 3-D wind and turbulence measurements from three steerable doppler lidars, IOP Conference Series: Earth and Environmental Science, 1, 12018, https://doi.org/10.1088/1755-1315/1/1/012018, 2008. a
Mikkelsen, T., Hansen, K. H., Angelou, N., Sjöholm, M., Harris, M., Hadley, P., Scullion, R., Ellis, G., and Vives, G.: Lidar wind speed measurements from a rotating spinner, in: European Wind Energy Conference and Exhibition, available at: http://www.orbit.dtu.dk (last access: 20 March 2018), 2010. a
Øye, S.: FLEX4 simulation of wind turbine dynamics, in: Proceedings of 28th IEA Meeting of Experts Concerning State of the Art of Aeroelastic Codes for Wind Turbine Calculations. Available through International Energy Agency, 71–76, Danmarks Tekniske Universitet, Lyngby, Denmark, 1996. a, b
Pedersen, M. M., Larsen, T. J., Larsen, G. C., Madsen, H. A., and Troldborg, N.: Turbulent wind field characterization and re-generation based on pitot tube measurements mounted on a wind turbine, in: 33rd Wind Energy Symposium, AIAA SciTech, American Institute of Aeronautics and Astronautics, Kissimmee, Florida, https://doi.org/10.2514/6.2015-1467, 2015. a
Pedersen, M. M., Larsen, T. J., Madsen, H. Aa., and Larsen, G. Chr.: Using wind speed from a blade-mounted flow sensor for power and load assessment on modern wind turbines, Wind Energ. Sci., 2, 547–567, https://doi.org/10.5194/wes-2-547-2017, 2017. a, b, c
Petersen, J. T. and Madsen, H. A.: Risø-R-993(EN): Local Inflow and Dynamics – Measured and Simulated on a Rotating Wind Turbine Blade, Risø National Laboratory, Roskilde, Denmark, 1997. a
Rahimi, H., Schepers, G., Shen, W. Z., García, N. R., Schneider, M., Micallef, D., Ferreira, C. S., Jost, E., Klein, L., and Herráez, I.: Evaluation of different methods for determining the angle of attack on wind turbine blades with CFD results under axial inflow conditions, Renew. Energ., available online 13 March 2018, in press, 2018. a
Schepers, J. G., Brand, A. J., Bruining, A., Hand, M., Infield, D., Madsen, H., Maeda, T., Paynter, J., van Rooij, R., and Shimizu, Y.: Final report of IEA Annex XVIII: enhanced field rotor aerodynamics database, Energy Research Center of the Netherlands, ECN-C-02-016, February, available at: ftp://ftp.ecn.nl/pub/www/library/report/2002/c02016.pdf (last access: 20 March 2018), 2002. a
Scholbrock, A. K., Fleming, P. A., Wright, A., Slinger, C., Medley, J., and Harris, M.: Field Test Results from Lidar Measured Yaw Control for Improved Power Capture with the NREL Controls Advanced Research Turbine, in: 33rd Wind Energy Symposium, AIAA SciTech Forum, American Institute of Aeronautics and Astronautics, Reston, Virginia, https://doi.org/10.2514/6.2015-1209, 2015. a
Shen, W. Z., Hansen, M. O. L., and Sørensen, J. N.: Determination of Angle of Attack (AOA) for Rotating Blades, available at: http://www.orbit.dtu.dk (last access: 20 March 2018), 2006. a
Shen, W. Z., Hansen, M. O. L., and Sørensen, J. N.: Determination of the angle of attack on rotor blades, Wind Energy, 12, 91–98, https://doi.org/10.1002/we.277, 2009. a
Simms, D. A., Hand, M. M., Fingersh, L. J., and Jager, D. W.: Unsteady aerodynamics experiment phases II-IV test configurations and available data campaigns, Tech. rep., National Renewable Energy Lab, available at: https://www.nrel.gov/docs/fy99osti/25950.pdf (last access: 20 March 2018), 1999. a
Snel, H. and Schepers, J. G.: Joint investigation of dynamic inflow effects and implementation of an engineering method, Netherlands Energy Research Foundation ECN, available at: https://www.ecn.nl/publications/E/1995/ECN-C–94-107 (last access: 20 March 2018), 1995. a
Snel, H., Houwink, R., Bosschers, J., Piers, W., van Bussel, G., and Bruining, A.: Sectional Prediction of 3-D Effects for Stalled Flow on Rotating Blades and Comparison with Measurements, in: Proc. of the European Community Wind Energy Conference, 395–399, Netherlands Energy Research Foundation ECN, Travemünde, Germany, 1993. a
Sørensen, J. N., and Shen, W. Z.: Numerical modelling of Wind Turbine Wakes, J. Fluids Eng.-T. ASME, 124, 393–399, https://doi.org/10.1115/1.1471361, 2002. a
Sørensen, J. N., Mikkelsen, R. F., Henningson, D. S., Ivanell, S., Sarmast, S., and Andersen, S. J.: Simulation of wind turbine wakes using the actuator line technique, Philos. T. R. Soc. A, 373, 20140071–20140071, https://doi.org/10.1098/rsta.2014.0071, 2015. a
Sørensen, N. N.: General Purpose Flow Solver Applied to Flow over Hills, PhD thesis, Technical University of Denmark, available at: http://www.orbit.dtu.dk (last access: 20 March 2018), 1995. a, b
Sørensen, N. N., and Aagaard Madsen, H.: Modelling of transient wind turbine loads during pitch motion, in: Proceedings (online) 2006 European Wind Energy Conference and Exhibition, Athens, Greece, 27 February–2 March 2006, vol. 27, 2006. a
St. Martin, C. M., Lundquist, J. K., Clifton, A., Poulos, G. S., and Schreck, S. J.: Wind turbine power production and annual energy production depend on atmospheric stability and turbulence, Wind Energ. Sci., 1, 221–236, https://doi.org/10.5194/wes-1-221-2016, 2016. a
Taylor, G. I.: The Spectrum of Turbulence, P. Roy. Soc. A-Math. Phy., 164, 476–490, https://doi.org/10.1098/rspa.1938.0032, 1938. a
Troldborg, N. and Meyer Forsting, A. R.: A simple model of the wind turbine induction zone derived from numerical simulations, Wind Energy, 20, 2011–2020, https://doi.org/10.1002/we.2137, 2017. a
Wagner, R., Vignaroli, A., Angelou, N., Sathe, A., Meyer Forsting, A. R., Sjöholm, M., and Mikkelsen, T. K.: Measurement of turbine inflow with a 3D windscanner system and a spinnerlidar, available at: http://www.orbit.dtu.dk (last access: 20 March 2018), 2015. a