the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Automatic measurement and characterization of the dynamic properties of tethered membrane wings
Dietmar Göhlich
Roland Schmehl
We have developed a tow test setup for the reproducible measurement of the dynamic properties of different types of tethered membrane wings. The test procedure is based on repeatable automated maneuvers with the entire kite system under realistic conditions. By measuring line forces and line angles, we determine the aerodynamic coefficients and lift-to-drag ratio as functions of the length ratio between power and steering lines. This nondimensional parameter characterizes the angle of attack of the wing and is varied automatically by the control unit on the towed test bench. During each towing run, several test cycles are executed such that mean values can be determined and errors can be minimized. We can conclude from this study that an objective measurement of specific dynamic properties of highly flexible membrane wings is feasible. The presented tow test method is suitable for quantitatively assessing and comparing different wing designs. The method represents an essential milestone for the development and characterization of tethered membrane wings as well as for the validation and improvement of simulation models. On the basis of this work, more complex maneuvers and a full degree of automation can be implemented in subsequent work. It can also be used for aerodynamic parameter identification.
- Article
(8755 KB) - Full-text XML
- BibTeX
- EndNote
With the turn of the millennium, kitesurfing has evolved into a mainstream water sport, followed by the more recent variants of land and snow kiting (Tauber and Moroder, 2013). In terms of industrial applications, flexible membrane wings have already been used since the 1970s as aerodynamic decelerators for airdrop systems and are currently being explored for airborne wind energy (AWE) generation (Schmehl, 2018). Despite the advancements within the kitesurfing and AWE industries, tethered membrane wings are mostly still designed by iterative testing with empirical and intuitive variation of wing parameters. Although this has led to a relatively high degree of maturity on the product level, the approach is time-consuming and expensive because a large number of prototypes need to be manufactured and tested. For this reason, we conclude that the empirical design method will only allow for limited further improvements and that it is indispensable to develop a systematic understanding of how wing performance parameters, such as aerodynamic coefficients, lift-to-drag ratio, steering forces and moments, depend on the wing design.
The empirical design method is used because compared to rigid wings the physics of flexible membrane wings are complex and the existing knowledge is limited due to deforming under aerodynamic load and steering line actuation. This holds particularly for leading edge inflatable (LEI) tube kites (see Fig. 1) and other single-skin kite types, since ram air wings have already been investigated systematically for several decades (Dunker, 2013, 2018; Johari et al., 2014).
Because of the high degree of flexibility and the low weight of the membrane structure, the flow around the wing and its shape are strongly coupled. A change in the flow field alters the aerodynamic load distribution to which the structure rapidly adjusts by deformation, which in turn changes the flow field. The fluid–structure coupling causes deformation phenomena at different length scales and timescales (Leuthold, 2015). A typical large-scale phenomenon is the spanwise bending and twisting of the entire wing due to steering line actuation. The ability of the membrane wing to deform asymmetrically and thereby generate a substantially increased turning moment makes it particularly suitable for AWE applications, which require excellent maneuverability (Breukels et al., 2013; Bosch et al., 2014; van Reijen, 2018; Fechner and Schmehl, 2018). Typical small-scale phenomena are the local flutter of the wing canopy or wrinkling, which is caused by local compression loads that cannot be supported by the woven fabric material.
Another characteristic that distinguishes flexible membrane wings from rigid wings is that the entire airborne system, consisting of a wing, tensile support system and in some cases also a suspended airborne control unit, is considerably larger for comparable traction force. This is due to the fact that a rigid wing can endure a much higher wing loading than a membrane wing and that it uses aerodynamic control surfaces with wing-integrated actuators that allow for a more compact design. For wind tunnel measurements large geometries are typically downscaled to fit into the test section of the tunnel. To ensure that the flow field is not affected by the scaling, the principle of dynamic similarity has to be enforced by maintaining a constant Reynolds number: . A common method to compensate for a decreasing chord length c is to increase the flow velocity v. However, downscaling a tethered membrane wing for wind tunnel testing is problematic because due to aeroelasticity the aerodynamic characteristics depend not only on the wing geometry but also on its deformation behavior. To account for this, the material properties of the wing and tether would have to be scaled accordingly, which is practically not feasible because the membrane is a woven fabric material that is partially arranged as a multilayer composite with rigid reinforcements, and the tether is a braided and coated line (Bosman et al., 2013).
A wind tunnel study of a small but full-scale ram air wing was presented by de Wachter (2008). The wing with a projected area of 5.2 m2 was suspended upside down in the test sections of two different large wind tunnels to determine the shape under aerodynamic load by photogrammetry and laser scanning. This shape was then used as a static boundary condition for steady CFD analysis, with the aim of assessing the computational prediction quality without the added complexity of the deforming membrane structure. The study contributed important knowledge about ram air wings at the lower end of the size range. In the same framework project, Bungart (2009) performed a coupled CFD and finite-element analysis of a ram air wing section, deriving aerodynamic coefficients and a deformed shape for the entire range of angle of attack. The analysis showed that the chambered design (chambers are separated by ribs, top skin and bottom skin; see Fig. 1) with upper and lower skin and the airfoil defined by a small number of ribs (connecting top skin and bottom skin) leads to ballooning. A similar effect can be observed with LEI tube kites, for which the canopy bulges out between the struts (inflatable tube providing structure) and, similar to the ribs, defines the design shape. It is obvious that these aeroelastic phenomena have to be taken into account by high-fidelity analyses. Subsequently, Breukels (2011) developed a multibody model and Bosch et al. (2014) a finite-element model of the flexible wing, bridle line system (line system that supports the wing structure and merges these lines into steering or power lines) and tether. In both approaches the same correlation derived by parametric CFD analysis is used to evaluate the aerodynamic load distribution as a function of angle of attack and wing deformation. While succeeding in simulating complete flight maneuvers relevant for AWE, the two studies did not include validations by wind tunnel experiments. It can be concluded that validated aeroelastic models of entire tethered membrane wings are neither available at present nor sufficiently fast to be used in the design process for which rapid iterations are required.
For this reason, less complex simulation models have been developed, describing the whole kite system as a point mass, a cluster of point masses (Fechner et al., 2015) or a rigid body (de Groot et al., 2011; Gohl and Luchsinger, 2013). These models do not explicitly describe the aeroelastic behavior of the wing and require as input the detailed aerodynamic properties of the kite system, including information about the steering behavior. In this respect, Erhard and Strauch (2013a, b), Fagiano et al. (2014), and Jehle and Schmehl (2014) have proposed empirical turn rate laws relating the turn rate of the wing to the steering input. The transition from a powered state (high angle of attack) to depowered state (low angle of attack) is covered by an empirical correlation (Fechner et al., 2015). According to Fagiano and Marks (2015), such lower-complexity models have already reached a quite mature state, but new insights appear to be difficult without experimental analysis.
However, despite the strong need for reproducible experimental data, only a few dedicated studies have been performed so far. Stevenson (2003) developed a tow test method to support the research and development of surf kites. The constant relative airflow was generated by driving the towing vehicle along a beach section. The data acquisition system recorded the lift-to-drag ratio as well as the lift coefficient both as functions of the ratio of the sum of steering line forces to total tensile force. Inspired by a method described by Stevenson et al. (2005), a simple stationary test setup for the beach was used by van der Vlugt (2010) to determine the lift-to-drag ratio of surf kites from the achievable flight speed when performing crosswind sweeps close to the ground. Dadd et al. (2010) described a tow test with the measurement rig mounted on a trailer such that it could be used for stationary and tow testing. A tow test experiment for the characterization of kites used as part of an AWE system was described by Costa (2011). Next to the movement of the kite and the line forces, the deformation was also measured using an image correlation system. Within the same framework project, Wood et al. (2017) presented a control strategy for flying figure-eight crosswind maneuvers during tow tests.
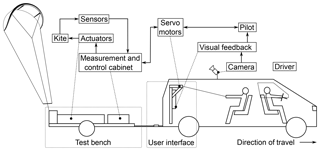
In none of the outlined test procedures was the manual control input recorded. However, for systematic aerodynamic parameter identification a recording of the steering inputs is crucial (de Groot et al., 2011; Mulder et al., 1994). We started the project TETA at TU Berlin with the aim of measuring the dynamic properties of kites under reproducible conditions for repeatable steering input (Hummel, 2017; Hummel and Göhlich, 2017). The developed test setup is suitable for the quantitative assessment of different types of tethered membrane wings and can be used stationary or moving at variable velocity to simulate different wind speeds as well as to reduce the influence of gusts.
This paper is organized as follows. Section 2 outlines the measurement concept and describes the detailed properties to be measured. In Sect. 3 the setup and design of the test bench is described, including the required sensor equipment. Section 4 continues with a brief overview of the data acquisition process. In Sect. 5 the experimental results are presented and discussed. In the conclusions, future research and improvements of the measurement concept and the implemented test bench are outlined.
A schematic side view of the tow test is illustrated in Fig. 2, including the aerodynamic lift and drag force components FL and FD, respectively, as well as the aerodynamic force FA.
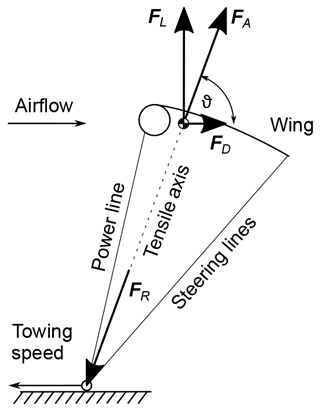
Figure 2Schematic side view of the tow test with the wing in steady-state equilibrium and effect of gravity neglected, i.e., mg=0, with and .
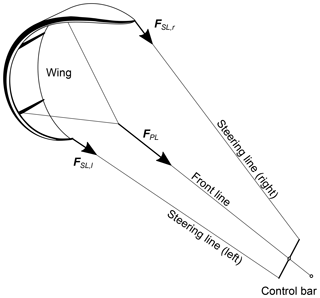
The resultant force acts in the center of pressure of the wing. A steady towing state is reached when the wing is no longer moving relative to the towing vehicle. In this state, the aerodynamic and gravitational forces acting on the wing are balanced by the tensile forces FPL, FSL,l and FSL,r acting in the power and steering lines. Because flexible lines cannot support bending loads these tensile forces are always aligned with the lines, as illustrated in Fig. 3.
The dashed line in Fig. 2 defines the tensile axis of the airborne system, which in the case of a negligible effect of gravity is aligned with the resultant force FR and inclined to the horizontal plane by the elevation angle ϑ.
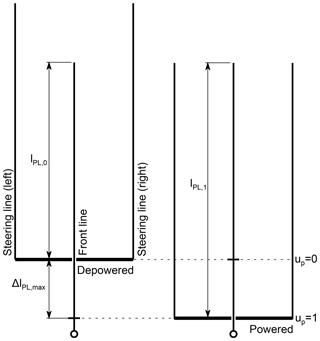
As illustrated in Fig. 3, the power line is attached to the towing point at the moving test rig. The flight behavior of the wing is controlled by a bar that can slide along the power line and attaches at its ends to the two steering lines. This setup is commonly used for kitesurfing and allows for the individual actuation of the left and right steering lines and changing the effective length of the power line. The effective length of the power line is defined as the distance between the kite attachment point and the control bar. For the “linear power” maneuver the control bar is automatically retracted along the power line. During this maneuver the effective length lPL of the power line changes from lPL,0 for the depowered state to lPL,1 for the powered state, as illustrated in Fig. 4.
Accordingly we define the relative power setting
which varies between up=0 for the depowered state and up=1 for the powered state. A similar nondimensional variable, the relative depower setting , was introduced by Fechner et al. (2015) to quantify the actuation of an airborne control unit suspended below the wing.
In the following we describe the wing properties that are used to characterize the flight dynamic behavior of the wing. Because the primary objective of the study was to achieve repeatable and reproducible measurements, we did not post-process the measured data further, for example, to account for line sag and the influence of weight. Since kites of the same size and the same control bar settings were tested at the same wind speed, a relative comparison of the wings is still possible.
2.1 Aerodynamic coefficients
The aerodynamic coefficients are nondimensional parameters that describe the aerodynamic properties of a wing. For a steady towing situation as illustrated in Fig. 2 we can determine the lift, drag and resultant aerodynamic coefficients of the entire system as
where ρ is the air density, A the surface area of the wing and va the apparent wind velocity. By definition the aerodynamic drag is aligned with the apparent wind velocity, and the aerodynamic lift is perpendicular.
Based on the resultant aerodynamic force coefficient we can determine the depower capability of the wing. This parameter can be calculated as the relative difference of maximum and minimum aerodynamic forces with
thus evaluating the entire range . For ground-generation AWE systems it is the traction force of the kite that is converted into electricity (Schmehl et al., 2013). For this variant of the technology, the kite is generally operated in consecutive pumping cycles and for maximizing the energy output, the resultant force coefficient CR has to be maximized during the traction phases and minimized during the retraction phases. For a flexible membrane wing, a good depower capability and flight stability are two conflicting design drivers (van der Vlugt et al., 2013).
2.2 Aerodynamic efficiency
The aerodynamic efficiency of a wing can be expressed as the ratio between the aerodynamic lift and drag force components. For a steady towing situation as illustrated in Fig. 2 the lift-to-drag ratio can be calculated from the elevation angle ϑ as
The lift-to-drag ratio is also a measure for the achievable flight speed of the kite in crosswind motion (van der Vlugt, 2010; Schmehl et al., 2013).
2.3 Tether forces
The tensile forces acting in the power and steering lines are shown in Fig. 3. The ratio of the steering line forces to the power line force,
characterizes the load distribution between the rear and front parts of the tethered wing, which allows for the validation of simulation approaches. Additionally, to characterize sport kites this parameter has so far been used intuitively to describe the perceived steering forces. Hence, a quantitative comparison of different wings regarding the load distribution between power and steering lines is feasible.
The following section gives a brief overview of the developed test bench. The main design goals are as follows: (1) using the entire kite system (including the unscaled kite and tether as well as the common steering input device) to generate realistic measurement data; (2) providing constant and controllable flow conditions; (3) allowing for repeatable and automated steering inputs; (4) permitting as little as possible of an impairment to the wing and its control unit by attachments; and (5) ensuring an easy transport and tow of the test bench. The final version of the test bench is shown in Fig. 5 and the schematic principle is illustrated in Fig. 6.
3.1 Structural design
With regard to the acquisition costs of the towed platform, a permanent mounting on a car trailer was decided. This solution allows us to use any given car for towing and thereby avoid additional costs. However, in contrast to heavier vehicles (e.g., four-wheeled vehicles with a driver's cab), the influence of oscillations into the test bench by the tethers is expected. This results in an additional requirement for the design of the test bench. All components are connected in such a way that it is possible to change the driving platform in the future to further improvements. For example, vibrations induced by the single-axle trailer could be greatly reduced by mounting the test rig on a heavier platform.
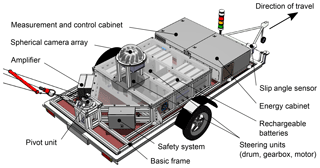
The basic frame is used to mount the test bench modules and absorb the load, in particular the line forces. It is assembled from aluminum profiles to avoid corrosion and easily afford subsequent design modifications. The kite is connected to the test bench by the pivot unit, which is located in the rear of the trailer (in relation to the direction of travel).
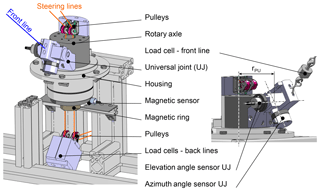
The pivot unit is shown in Fig. 7. It is designed to have a minimum inertia, which allows for a smooth untwisting of the lines. This leads to an automatic alignment of the line connection points towards the direction of the power line and thus towards the direction of the wing within the wind window. The required torque for untwisting is realized by the tensile force acting on the power line. The steering lines of the test bench are connected to the ends of the control bar and passed through the center of the rotary axle to realize minimal inertia. They are redirected by pulleys connected to rope drums that are operated by motors (see Fig. 5, steering units). The tether forces are measured by means of load cells in the steering lines, not interconnecting the lines. A magnetic sensor attached to the static part measures the rotation of a magnetic ring and thus of the unit itself. The rotary part essentially consists of the rotary axle. The universal joint is attached to it, transmitting the force of the power line.
Each steering unit, which controls the length of a steering line, consists of a cable drum, a gearbox and a motor. The motors are each operated by a servo controller located within the measurement and control cabinet. The steering units are located in the middle of the test bench, together with the batteries. Since the motors and batteries are the heaviest components of the test rig, this arrangement allows the center of gravity to be close to the wheel axis to prevent a static tilting of the trailer (unavoidable tilting of the trailer is measured by an inertial sensor to correct the elevation angle described in Sect. 3.2). The design force was set to 5000 N. In the front area in the direction of travel, space was provided for the control cabinets.
3.2 Sensor systems
This section gives a brief overview of the sensor technology used to achieve the measuring results, which are described in Sect. 5. Components are termed as a sensor system, which serves the purpose of determining certain measuring variables and for which a clear distinction from the overall system is possible. For a complete documentation of all sensor systems please refer to Hummel (2017).
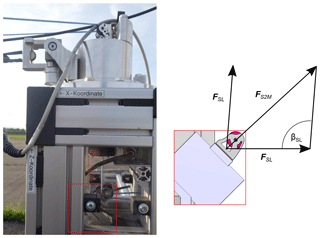
The exact measurement of the line forces is highly prioritized due to the requirements for the majority of kite properties (see Sect. 2). To avoid impairments caused by additional masses of the load cells within the steering lines, the load cells are installed without insertion. Furthermore, this also enables the use of load cells with a higher accuracy, which is related to a higher mass of the load cells (HBM S2M, precision class of 0.02 %, nominal force 1000 N, which results in an absolute error of N). The resultant forces FS2M can be obtained from Eq. (8), as illustrated in Fig. 8, assuming that the friction of the pulley is negligible. As shown in Eq. (8), the relation between the force measured at the load cell and the force acting on the steering lines is linear. This is caused by the constant line angle βSL. With the maximum measurable force within the steering lines is 707 N. Field tests have shown that this value is high enough for common wing sizes. If a higher maximum force is required in the future, the load cells can be exchanged by sensors with a higher nominal force. However, this will be accompanied by reduced accuracy:
The measurement of the force in the power line is performed by an interposition of the load cell (see Fig. 7). A load cell with a nominal force of 5000 N is used, which has a precision class of 0.2 % (HBM U9C). The absolute error results in N. The signals of the load cells are amplified and then sent to an extension board of the sbRIO. The amplifiers are located as shown in Fig. 5.
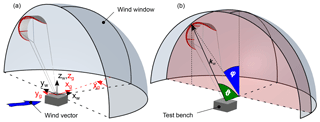
Measuring the angle of the power line is intended to enable a simple and reliable determination of the elevation angle ϑ and the azimuth angle φ, which is illustrated in Fig. 9. The polar coordinate system, in particular the elevation angle ϑ, is based on Erhard and Strauch (2013a). The definition of the elevation angle is suited for determining the aerodynamic efficiency, even if the kite is not located within the x–z plane in reference to the wind direction. In contrast to other definitions, i.e., β in Schmehl et al. (2013), ϑ does not vary for a constant glide ratio (see Fig. 9, intersection of red plane with grey wind window). This angle definition facilitates the calculation of the glide ratio even if the kite occasionally deflects from the symmetry plane of the wind window (downwind position). The rotary axle has a non-neglecting rotational inertia and therefore the measurement of the azimuth and elevation angle, with respect to the test bench, is composed of three sensors, which are shown in Fig. 7. First, the rotational deviation within the x–y plane is calculated by the sum of the rotation angle of the rotary axle ΦRA (measured by the magnetic sensor) and the measured wind direction Xg. The magnetic ring of the magnetic sensor has a sufficiently large inner diameter to pass the steering lines through it. Thus, it is possible to mount it underneath the rotary axle without impairing the functionality of the pivot unit. Second, the rotational deviation of the universal joint is measured by the elevation angle sensor (ΘUJ) and the azimuth angle sensor (ΦUJ) to realize low friction as well as a negligible influence on the line angle. As a result, the universal joint will already deflect at low forces in the power line.
The wing position kw within the wind window can be calculated by Eq. (11) as a result of the sensors; index “g” indicates the reference to the test bench and index “w” to the wind direction coordinate system:
Here, r represents the tether length and rPU represents the distance between the axis of the rotary axle and the pivot point of the universal joint (see Fig. 7). From Eq. (12) the resulting elevation angle ϑw and azimuth angle φw can be determined:
3.3 Error analysis
The error analysis of the measured data leading to the results in Sect. 5 is described hereafter.
3.3.1 Wind speed
The absolute error of the wind speed measurement for the weather station according to the manufacturer is εvw=0.05 m s−1. The error of the wind direction measurement is given by .
For calculating the kite properties, the resulting wind speed at kite level is needed, whereas the wind speed on top of the towing vehicle is measured. Thus, as an additional error for the given test setup, the error due to the height difference in wind measurement, must be investigated. The weather station is located on top of the towing vehicle at a height zREF of 3 m. Depending on the length of the tether, the kite typically reaches a height z of 15 to 30 m. The most commonly used extrapolation method is the wind power law (Akdağ et al., 2013; Ghita et al., 2013). This method is assumed to be valid within the ground-level boundary layer (<100 m). Empirical data presented by Archer (2013) show that this model is well suited to approximate wind profiles by measuring at a reference height zREF and thus to estimate the wind speed vtw,plaw(z) on kite level z. The wind power law is defined as follows:
Here, vtw(zREF) indicates the static true wind speed at a fixed position above the ground at an altitude zREF (index “tw”: true wind speed), which also cannot be directly measured because of the moving test bench. The coefficient of friction α depends on the terrain type and increases with rising terrain roughness. Despite testing on a former airfield, the coefficient of friction is assessed in an overestimating way to perform a safe calculation (this overestimation will result in an overestimated static wind speed on kite level, which in turn will result in an overestimation of the resulting error δvw,real). Thus, it is assumed as 0.25 for wooded countryside with many trees. If the true wind vector vtw(zREF) points towards the opposite direction of travel, the influence of the relative error δvw,real of the wind speed vw,real(z) at kite level will be at a maximum. This is because the relative portion of the true wind speed vtw(zREF) is maximized and the required speed of the towing vehicle vp(zREF) to reach the desired testing speed vw(zREF) is minimized:
The resulting wind speed vw,real at flight altitude z is composed of the traveling speed vp and the theoretical wind speed according to the wind power law vtw,plaw(z), leading to
The resulting error is reduced with decreasing altitude, decreasing natural wind and increasing target speed. At present, line lengths of 24 m are used, while the minimum target speed is set to 11 m s−1. The relative error can thus be assumed as %. For a detailed calculation please refer to Hummel (2017).
3.3.2 Elevation angle
The angle sensors of the universal joint have an absolute measuring error of , while the magnetic sensor has an absolute measuring error of . To determine the resultant error from the three angle sensors, the error-prone angles ϑ and φ must be calculated analogously to Sect. 3.2. The maximum error was determined using a MATLAB script. At first, the error-free angles were calculated, followed by a calculation of the error-prone angles for each angle combination. These error-prone angles result from a combination of the minimum and maximum values, which arise due to the individual errors mentioned before. The maximum error of the elevation angle in the coordinate system of the test bench is . If the error of the weather station is added to the error of the magnetic sensor εΦRA, the theoretical maximum error of the elevation angle within the wind direction coordinate system results in .
The quality of the analysis could be further improved by accounting for line sag and the influence of weight. Nevertheless, as mentioned in Sect. 2, we did not post-process the measured data because the primary objective of the study was the repeatability and reproducibility of the measurements.
3.4 User interface
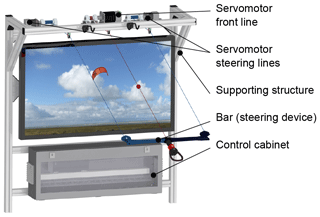
The developed user interface (bar stand) allows us to manipulate the control bar position of the test bench. The pilot also receives a haptic feedback of the line forces via the interface. The system was designed based on the assumption that an increase in safety and reliability is achieved through an improved perception of the prevailing flight condition, when a fully or semi-manual flight is performed. The pilot should be able to estimate the line forces without numerical display elements to extend the pilot's perception of the flight situation. As a result, this device allows for the subjective evaluation of the kite properties.
The user interface is located inside the towing vehicle and equipped with a common control bar used to control sport kites (see Fig. 10). The measured line forces are induced to the lines of the user interface by means of winches operated by servomotors. The force acting on the power line is transferred to the pilot via a harness used for kitesurfing. The motor position and thus the current bar position is determined by integrated encoders. This setup enables a control of the wing, which is close to reality, by moving a common control bar as well as by transmitting the scaled forces acting on the lines. The maximum force of the steering lines was set to 50 N and the force of the power line to 350 N. This determination was made to avoid a physical overstressing of the pilot and to limit the size of the actuators. The measured line forces must therefore be scaled by a proportionality factor.
The visual feedback is realized by the display shown in Fig. 10. Because of the integration of the user interface into the towing vehicle a direct view of the wing is impossible. The image is taken by means of a wide-angle camera atop the roof of the vehicle. To enable a subsequent video evaluation, the recorded data are stored on the camera's internal memory card. When the measurement procedure is started by the pilot, video recording is initiated automatically by the sbRIO (central control unit; see Sect. 4.1). An LED is placed within the visual range of the camera for the later synchronization of the video and the measured data. This enables the synchronization of the beginning of data recording with the beginning of the video.
To record the measurement data acquired from the sbRIO and perform control inputs to set up the test run, a notebook is used as a host computer. The host computer communicates with the sbRIO via network interface. During a test run, the notebook is placed in front of the pilot so that a perception of the numerical display elements of the host computer is possible. During a test procedure the pilot is not required to execute inputs on the host computer.
Furthermore, a foot pedal connected to the host computer is used to execute maneuvers in the testing mode. When the pedal is actuated by the pilot, the previously set maneuver is executed by the sbRIO. Depending on the degree of automation, the pilot is enabled to act out certain steering inputs via the control bar. As soon as the pilot releases the pedal, the maneuver is terminated and the kite can be controlled manually again.
4.1 Data processing system
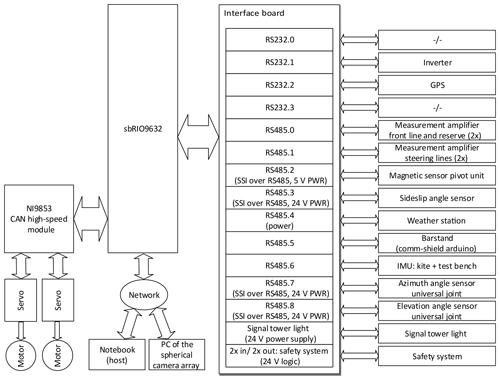
This section briefly describes the structure of the data processing hardware of the test bench. A schematic diagram is shown in Fig. 11. The data processing system and the DC power supply are localized within the measurement and control cabinet (see Fig. 5). As shown in Fig. 11, the National Instruments sbRIO 9632 serves as the central control unit. It is connected to various components, such as sensors, via a self-made custom interface board. The servo controllers of the motors mentioned in Sect. 3.1 communicate via a CAN module with the sbRIO. A network interface is used to communicate with the host computer and retrieve measured values of the spherical camera array. The sbRIO has been chosen because of the implemented central processing unit (CPU) and the field-programmable gate array (FPGA).
The CPU allows the main control algorithm (the real-time operating system; RTOS) to be executed in real-time. To ensure a safe test operation, a real-time capability is required. In particular, control inputs have to be executed in a predefined time. For this purpose, a deterministic loop was introduced within the RTOS (with a maximum execution period of 20 ms). This allows the motors to be addressed at a frequency of 50 Hz. The FPGA processor, on the one hand, is used as an access to the analog and digital interfaces via the internal bus of the sbRIO. On the other hand, programs can be implemented that are converted into a logic circuit by means of the integrated gates. Due to the configurable logic circuit, parallel signal processing is possible, which increases the speed of the data processing.
4.2 Experimental setup
The dynamic test procedure used in this paper is described below. Dynamic tests are characterized by moving the test bench. The procedure can be carried out on any straight track. It is of paramount importance that the ground surface is as flat as possible to reduce oscillations. The measurements within this work have been carried out on the former airport Pütnitz, Germany. The target wind speed was consistently set to 22 kn (11.3 m s−1) to demonstrate the repeatability of the test method.
The range of wind speed that can be examined is only limited by the cut-in wind speed of the kite (minimum wind speed for flying the kite) and the maximum tensile force resulting from the kite acting on the test bench (the design force was set to 5000 N; see Sect. 3.1). Because of the weight of the test bench the maximum vertical force is currently limited to 3000 N, which could be increased by using a heavier trailer. Assuming a coefficient of CR=0.7 (representing the peak value in Fig. 15), surface area of A=10 m2, air density of ρ=1.184 kg m−3 and apparent wind velocity of va=50 kt (25.7 m s−1), the resulting force is FR=2837 N <3000 N (see Eq. 4). Since the aerodynamic coefficients investigated so far are wind independent, there is no need to test in higher wind speeds to compare the wings against each other. For the presented maneuver “linear power” in combination with the presented wing sizes, a maximum testing speed of 50 kn (25.7 m s−1) can be given. The traction force will increase substantially when the kite is operated in crosswind maneuvers (Schmehl et al., 2013). To analyze kites in this flight mode with traction forces exceeding 5000 N, the design of the test bench has to be adapted or the surface area of the wing has to be reduced accordingly.
Figure 12 shows the towing vehicle with the test bench in measuring operation. Measurements are solely conducted on the straight sections. As described above, tests are carried out on days with as little wind as possible. Testing under these conditions allows for the performance of multiple maneuvers without landing the kite since the track can be run both ways.
To launch the kite, it is set up behind the towing vehicle, placed on its trailing edge and the lines are tightened. When accelerating the test bench, the kite does an ascent movement in the direction of the zenith. The driver of the vehicle is supplied with a display showing the duplicated view of the host computer. That way, the driver can assess the current flight situation and the currently measured wind speed. The driver adjusts the desired wind speed via the cruise control of the towing vehicle. After reaching the target speed, the maneuvers can be carried out.
4.3 Measurement data evaluation
The measurement data are evaluated by means of the software Diadem, which is originated by the company National Instruments, also supplying the software for the host as well as the measurement and control unit.
The implemented script is used to preprocess, process and display the measurement data. First, the desired measurement files are transferred to the script. Then, each measurement file is preprocessed in a loop. This includes, among other functions, an automatic detection of maneuvers and a distinction between driving along the straight track and turnaround. To obtain the desired graphs, statistical values are calculated from the maneuvers. The graphs and an overview of the measured data are then added to a report PDF for each measurement file. Once each measurement file has been processed, the results are summarized in an additional overview to allow for a comparison between each file.
This section presents the obtained results for the wing properties defined in Sect. 2. The measurements were taken by means of the maneuver “linear power” to demonstrate the functionality of the test bench and the feasibility of the developed test procedure. Before starting the maneuver, the wing is positioned and stabilized by the pilot at the zenith position within the wind window. The foot pedal connected to the host computer is then manually actuated to launch the maneuver. The power position is automatically increased by the sbRIO up to ΔlPL,max=500 mm (see Fig. 4) with a constant speed over a period of 4.5 s. The pilot can still execute steering inputs to keep the kite in a stable position at the zenith.
The measurement diagrams are shown in the following subsections. Only maneuvers lasting a given minimal time span were taken into account. During some maneuvers an unintentional change in position or orientation (e.g., caused by gusts) led to the pilot aborting the maneuver; this can result in a too-short maneuver, which in turn would make the statistical value calculation impossible. The valid results are plotted against the power ratio up. The determination of the angle of attack was not feasible within the scope of this work and will be done in future research for this project.
5.1 Tested kites
For characterization of the dynamic properties, five different kites with the same surface area of 10 m2 were measured (denoted by kite A to E within the graphs). All kites are designed for different purposes in kite sports.
On the one hand, kite C was designed to ride efficiently upwind, i.e., affording a high traveling angle in the wind direction. In addition, high jumps with a long air time should be possible. Therefore, a high aerodynamic efficiency associated with a high resulting force is required. Furthermore, this kite should provide a high depower capability, resulting in a significant change in the lift coefficient.
Kites D and E have the same design, but originated from different model years. Because of their shape, these kites feature a significant contrast to the other kites. Significantly more wing area is located at the wing tips, which should result in lower aerodynamic efficiency and a lower lift coefficient.
Kite A is intended to be an all-rounder, which means the resulting lift and efficiency should be positioned between C and D–E.
Kite B is designed to achieve good handling and turning abilities as well as providing a good upwind performance at the same time. For this reason the steering forces have to be higher while depowered (up≃0) compared to the other kites.
The measurements were conducted during two different days (marked as day 1 and 2). For each property, a figure is shown that summarizes all measurement data into a single curve for each kite to compare the kites against each other. Additionally, these figures show the resulting error from all maneuvers that were taken into account for a confidence interval of 95 %.
5.2 Aerodynamic efficiency
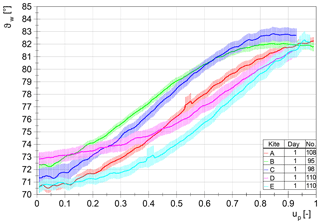
The measurement results of the elevation angle ϑw can be seen in Fig. 13. The resulting aerodynamic efficiency can be calculated by Eq. (6) (see Fig. 14). The different curves can be distinguished by height and progression.
As discussed in the previous chapter, it can be shown that kite C offers the highest and kites D–E the lowest aerodynamic efficiency. It can also be concluded that a reliable repeatability within the same day can be achieved. This finding was confirmed by further tests on different days. The only significant deviation was found after a long period between two test runs. The time between day 1 and day 2 was exactly 1 year. The elevation angle differs between these days only by an offset. To determine this offset in the future and, if necessary, to compensate for it, a reference kite was introduced, which is measured once every test day. The resulting curves of this reference kite should fit each other on different test runs. If an offset occurs, the starting points of the graphs can be corrected and thus the wings can still be compared relatively to each other. To fully compensate for this deviation in the future, the initial horizontal alignment of the test bench will be measured by means of an inertial measurement unit. The deviation is most likely caused by changes in geometry being difficult to control, for example a change in the tire pressure of the trailer or the towing vehicle.
5.3 Lift coefficient
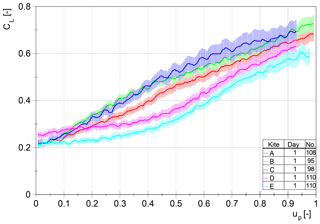
The lift coefficient CL is calculated according to Eq. (2) using the given manufacturer's surface area of 10 m2 and a constant air density of ρ=1.184 kg m−3. The airflow velocity is assumed as equal to the measured wind speed of the weather station. The total tether force is calculated by the sum of the measured forces of three load cells. Due to the high elevation angles, the resulting force coefficient CR resembles CL and is not shown separately (see Eqs. 4 and 2 with ).
The resulting curves of the datasets are shown in Fig. 15. As predicted in Sect. 5.1, kite C offers the highest and kites D–E the lowest lift coefficient. The deviation between datasets for the same kite lies within the resulting error. The influence of the abovementioned deviation of the elevation angle measurement on the lift coefficient is negligible.
As mentioned in Sect. 2.1, the depower capability for each kite can be calculated by the difference between the maximum and minimum values. Apparently, kites B and C are best suited for AWE systems using the pumping mode because of their high depower capability and their high lift coefficient. A further distinction can be made based on the curve progressions. Kites A to C can be characterized by their degressive progression, whereas kites D and E are characterized by a progressive increase in the lift coefficient.
5.4 Force ratio
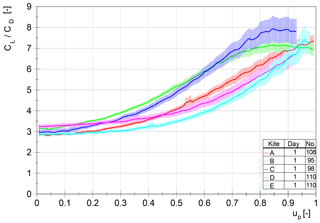
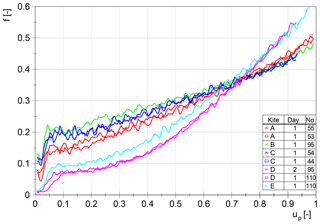
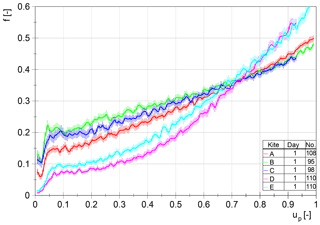
Figures 16 and 17 show the force ratio f between steering lines and the power line, which can be calculated by Eq. (7).
To estimate the reproducibility for each kite property, all eight datasets are first presented together within the same diagram (Fig. 16). Obviously, a distinction between the kites is possible. As a result of their different wing shapes, the curve progression of kites D and E compared to the other kites is clearly different (progressive). Furthermore, the kites can be distinguished by the height of the force ratio. With these curves and the force curve itself, existing simulation models can be evaluated reliably.
For AWE systems the force ratio is of great importance, since it determines the steering possibility of the wing while fully depowered (especially during the retraction phase). To guarantee the execution of control commands by transmitting the steering forces, the force ratio must not be too low.
In most cases, a reproducible, high-quality measurement of the flight dynamic properties of tethered flexible membrane wings exceeds the available budget. Furthermore, existing approaches do not allow for a recording or even automation of steering inputs, which is crucial for the reproducibility of the experiment. In this paper, we have presented a unique tow test setup for automatic measurement of the dynamic properties of different wing types at full scale and under realistic conditions. The objective was to demonstrate the methodology and particularly the repeatability of the test procedure. Using the maneuver “linear power”, we determine the aerodynamic coefficients and lift-to-drag ratio of the wing as functions of the ratio of power and steering line lengths – denoted as the relative power setting – by measuring line forces and line angles. The ratio is varied automatically, while the pilot is manually adjusting the steering line lengths to keep the kite at a fixed position relative to the towing vehicle. By automating the test cycles we can acquire mean values of high statistical quality with minimal errors. We have demonstrated repeatability on the basis of eight recorded datasets using the maneuver “linear power” at a constant wind speed of 22 kn (11.3 m s−1). We conclude from this study that it is feasible to objectively measure the flight dynamic properties of tethered membrane wings and to quantitatively assess and compare different wing designs.
Based on this work, we propose several functional enhancements for future research. By performing more sophisticated flight maneuvers the full operational envelope of airborne wind energy systems can be covered. By completing the automation of the process we expect a significant increase in measurement accuracy, which will improve the future aerodynamic parameter identification and evaluation of existing simulation models. A further accuracy increase can be achieved by adding sensors to the wing and directly measuring the flight state and the relative flow.
The code and measurement data can be made available in the framework of a cooperation agreement. If interested please contact the corresponding author.
JH designed the test setup with the support of DG and performed the measurements. The preparation of the paper was the joint work of JH, DG and RS.
The authors declare that they have no conflict of interest.
Roland Schmehl has received funding from the European Union Horizon 2020
research and innovation program under Marie Skłodowska-Curie grant
agreement no. 642682 for the ITN project AWESCO and grant agreement no.
691173 for the “Fast Track to Innovation” project REACH.
Edited by: Johan Meyers
Reviewed by: Julien
Deparday and one anonymous referee
Akdağ, S. A., Güler, Ö., and Yağci, E.: Wind speed extrapolation methods and their effect on energy generation estimation, in: Renewable Energy Research and Applications (ICRERA), Madrid, Spain, 20–23 October 2013, https://doi.org/10.1109/ICRERA.2013.6749793, 2013. a
Archer, C. L.: An Introduction to Meteorology for Airborne Wind Energy, in: Airborne Wind Energy, edited by: Ahrens, U., Diehl, M., and Schmehl, R., Green energy and technology, chap. 5, Springer, Berlin Heidelberg, 81–94, https://doi.org/10.1007/978-3-642-39965-7_5, 2013. a
Bosch, A., Schmehl, R., Tiso, P., and Rixen, D.: Dynamic nonlinear aeroelastic model of a kite for power generation, J. Guid. Control Dynam., 37, 1426–1436, https://doi.org/10.2514/1.G000545, 2014. a, b
Bosman, R., Reid, V., Vlasblom, M., and Smeets, P.: Airborne Wind Energy Tethers with High-Modulus Polyethylene Fibers, in: Airborne Wind Energy, edited by: Ahrens, U., Diehl, M., and Schmehl, R., Green Energy and Technology, chap. 33, Springer, Berlin Heidelberg, 563–585, https://doi.org/10.1007/978-3-642-39965-7_33, 2013. a
Breukels, J.: An Engineering Methodology for Kite Design, PhD thesis, Delft University of Technology, ISBN: 978-90-8891-230-6, available at: http://resolver.tudelft.nl/uuid:cdece38a-1f13-47cc-b277-ed64fdda7cdf (last access: 19 January 2019), 2011. a
Breukels, J., Schmehl, R., and Ockels, W.: Aeroelastic Simulation of Flexible Membrane Wings based on Multibody System Dynamics, in: Airborne Wind Energy, edited by: Ahrens, U., Diehl, M., and Schmehl, R., Green Energy and Technology, chap. 16, Springer, Berlin Heidelberg, 287–305, https://doi.org/10.1007/978-3-642-39965-7_16, 2013. a
Bungart, M.: Fluid-Struktur Kopplung an einem RAM-Air-Kiteschirm, Master's thesis, University of Stuttgart, 2009. a
Costa, D.: Experimental Investigation of Aerodynamic and Structural Properties of a Kite, Master's thesis, ETH Zurich, 2011. a
Dadd, G. M., Hudson, D. A., and Shenoi, R. A.: Comparison of two kite force models with experiment, J. Aircraft, 47, 212–224, https://doi.org/10.2514/1.44738, 2010. a
de Groot, S. G. C., Breukels, J., Schmehl, R., and Ockels, W. J.: Modelling Kite Flight Dynamics Using a Multibody Reduction Approach, J. Guid. Control Dynam., 34, 1671–1682, https://doi.org/10.2514/1.52686, 2011. a, b
de Wachter, A.: Deformation and Aerodynamic Performance of a Ram-Air Wing, Master's thesis, Delft University of Technology, available at: http://resolver.tudelft.nl/uuid:786e3395-4590-4755-829f-51283a8df3d2 (last access: 19 January 2019), 2008. a
Dunker, S.: Ram-Air Wing Design Considerations for Airborne Wind Energy, in: Airborne Wind Energy, edited by: Ahrens, U., Diehl, M., and Schmehl, R., Green Energy and Technology, chap. 31, Springer, Berlin Heidelberg, 517–546, https://doi.org/10.1007/978-3-642-39965-7_31, 2013. a
Dunker, S.: Tether and Bridle Line Drag in Airborne Wind Energy Applications, in: Airborne Wind Energy – Advances in Technology Development and Research, edited by: Schmehl, R., Green Energy and Technology, chap. 2, Springer, Singapore, 29–56, https://doi.org/10.1007/978-981-10-1947-0_2, 2018. a
Erhard, M. and Strauch, H.: Theory and Experimental Validation of a Simple Comprehensible Model of Tethered Kite Dynamics Used for Controller Design, in: Airborne Wind Energy, edited by: Ahrens, U., Diehl, M., and Schmehl, R., Green Energy and Technology, chap. 8, Springer, Berlin Heidelberg, 141–165, https://doi.org/10.1007/978-3-642-39965-7_8, 2013a. a, b
Erhard, M. and Strauch, H.: Control of Towing Kites for Seagoing Vessels, IEEE T. Contr. Syst. T., 21, 1629–1640, https://doi.org/10.1109/TCST.2012.2221093, 2013b. a
Fagiano, L. and Marks, T.: Design of a Small-Scale Prototype for Research in Airborne Wind Energy, IEEE-ASME T. Mech., 20, 166–177, https://doi.org/10.1109/TMECH.2014.2322761, 2015. a
Fagiano, L., Zgraggen, A. U., Morari, M., and Khammash, M.: Automatic crosswind flight of tethered wings for airborne wind energy:modeling, control design and experimental results, IEEE T. Contr. Syst. T., 22, 1433–1447, https://doi.org/10.1109/TCST.2013.2279592, 2014. a
Fechner, U. and Schmehl, R.: Flight Path Planning in a Turbulent Wind Environment, in: Airborne Wind Energy – Advances in Technology Development and Research, edited by: Schmehl, R., Green Energy and Technology, chap. 15, Springer, Singapore, 361–390, https://doi.org/10.1007/978-981-10-1947-0_15, 2018. a
Fechner, U., van der Vlugt, R., Schreuder, E., and Schmehl, R.: Dynamic Model of a Pumping Kite Power System, Renew. Energ., 83, 705–716, https://doi.org/10.1016/j.renene.2015.04.028, 2015. a, b, c
Ghita, M. R., Andrei, H., and Marin, O. F.: Modeling of wind resource to the turbine hub height, in: Proceedings of the International Conference on Electronics, Computers and Artificial Intelligence (ECAI), IEEE, Pitesti, Romania, 27-29 June 2013, 1–6, https://doi.org/10.1109/ECAI.2013.6636175, 2013. a
Gohl, F. and Luchsinger, R. H.: Simulation Based Wing Design for Kite Power, in: Airborne Wind Energy, edited by: Ahrens, U., Diehl, M., and Schmehl, R., Green Energy and Technology, chap. 18, Springer, Berlin Heidelberg, 325–338, https://doi.org/10.1007/978-3-642-39965-7_18, 2013. a
Hummel, J.: Automatisierte Vermessung und Charakterisierung der dynamischen Eigenschaften seilgebundener, vollflexibler Tragflächen, Dissertation, Technische Universität Berlin, Berlin, https://doi.org/10.14279/depositonce-5863, 2017. a, b, c
Hummel, J. and Göhlich, D.: Automatic Measurement and Characterization of the Dynamic Properties of Tethered Flexible Wings, in: Book of Abstracts of the International Airborne Wind Energy Conference 2017, edited by: Diehl, M., Leuthold, R., and Schmehl, R., University of Freiburg & Delft University of Technology, Freiburg, Germany, 126–127, available at: http://resolver.tudelft.nl/uuid:89050243-6bc6-4e25-88f1-dcf4f6145bfe (last access: 19 January 2019), 2017. a
Jehle, C. and Schmehl, R.: Applied Tracking Control for Kite Power Systems, J. Guid. Control Dynam., 37, 1211–1222, https://doi.org/10.2514/1.62380, 2014. a
Johari, H., Yakimenko, O., and Jann, T.: Aerodynamic Characterization of Parafoils, in: Precision Aerial Delivery Systems: Modeling, Dynamics, and Control, edited by: Yakimenko, O. A., Progress in Astronautics and Aeronautics, chap. 4, American Institute of Aeronautics and Astronautics, Inc., 199–261, https://doi.org/10.2514/5.9781624101960.0199.0262, 2014. a
Leuthold, R. C.: Multiple-Wake Vortex Lattice Method for Membrane Wing Kites, Master's thesis, Delft University of Technology, http://resolver.tudelft.nl/uuid:4c2f34c2-d465-491a-aa64-d991978fedf4(last access: 19 January 2019), 2015. a
Mulder, J. A., Sridhar, J. K., and Breeman, J. H.: Identification of Dynamic Systems: Applications to Aircraft, Part 2, Nonlinear Analysis and Manoeuvre Design, in: RTO AGARDograph 300: Flight Test Technique Series, vol. 3, Advisory Group for Aerospace Research and Development (AGARD), Neuilly sur Seine, available at: https://www.sto.nato.int/publications/AGARD/AGARD-AG-300-3-II/AGARDAG300.pdf (last access: 19 January 2019), 1994. a
Schmehl, R. (Ed.): Airborne Wind Energy – Advances in Technology Development and Research, Green Energy and Technology, Springer Nature, Singapore, https://doi.org/10.1007/978-981-10-1947-0, 2018. a
Schmehl, R., Noom, M., and van der Vlugt, R.: Traction Power Generation with Tethered Wings, in: Airborne Wind Energy, edited by: Ahrens, U., Diehl, M., and Schmehl, R., Green Energy and Technology, chap. 2, Springer, Berlin Heidelberg, 23–45, https://doi.org/10.1007/978-3-642-39965-7_2, 2013. a, b, c, d
Stevenson, J., Alexander, K., and Lynn, P.: Kite performance testing by flying in a circle, Aeronaut. J., 109, 269–276, https://doi.org/10.1017/S0001924000000725, 2005. a
Stevenson, J. C.: Traction Kite Testing and Aerodynamics, PhD thesis, University of Canterbury, available at: http://hdl.handle.net/10092/7688 (last access: 19 January 2019), 2003. a
Tauber, M. and Moroder, P.: Kite Surfing and Snow Kiting, in: Adventure and Extreme Sports Injuries: Epidemiology, Treatment, Rehabilitation and Prevention, edited by: Mei-Dan, O. and Carmont, M. R., chap. 8, Springer, London, 173–187, https://doi.org/10.1007/978-1-4471-4363-5_8, 2013. a
van der Vlugt, R.: Aero- and Hydrodynamic Performance Analysis of a Speed Kiteboarder, Master's thesis, Delft University of Technology, available at: http://resolver.tudelft.nl/uuid:9e0c7a62-149c-4fab-8d27-afe15c1a8795 (last access: 19 January 2019), 2010. a, b
van der Vlugt, R., Peschel, J., and Schmehl, R.: Design and Experimental Characterization of a Pumping Kite Power System, in: Airborne Wind Energy, edited by: Ahrens, U., Diehl, M., and Schmehl, R., Green Energy and Technology, chap. 23, Springer, Berlin Heidelberg, 403–425, https://doi.org/10.1007/978-3-642-39965-7_23, 2013. a
van Reijen, M.: The Turning of Kites: A Quantification of Known Theories, Master's thesis, Delft University of Technology, available at: http://resolver.tudelft.nl/uuid:5836c754-68d3-477a-be32-8e1878f85eac (last access: 19 January 2019), 2018. a
Wood, T. A., Hesse, H., and Smith, R. S.: Predictive Control of Autonomous Kites in Tow Test Experiments, IEEE Control Systems Letters, 1, 110–115, https://doi.org/10.1109/LCSYS.2017.2708984, 2017. a